分類を行った。洗掘の主因である河床面の円柱まわりに形成される馬蹄形渦の 高さHsに着目した。堀中4)は流れの可視化から水深hoとHsの関係を調べた。 図1に示すho/D >12のときはHs=06D, ho/D ≤ 12のときはHs=05hoを 得た。 五十嵐3)は最終洗掘深さも水深依存タイプ(ho/D ≤ 12)と円柱直径ここでは、負荷を慣性モーメントの計算ができる単純な形に近似していくつかの要素に置き換え、それらの慣性モーメントの合計を求めます。 以下に慣性モーメントの計算でよく用いる物体とその計算式を示します。 図⑤ の様 円柱 中心が回転 からx · 慣性体が円柱、または中空円柱ならJx 0 は上記の円柱、または中空円柱のJxまたはJy の計算式に置き換えます。m・l 2 は変わりません。 回転する負荷慣性モーメントはこれらの丸か四角の計算式で対応できています。 直線運動する負荷慣性モーメントは以下
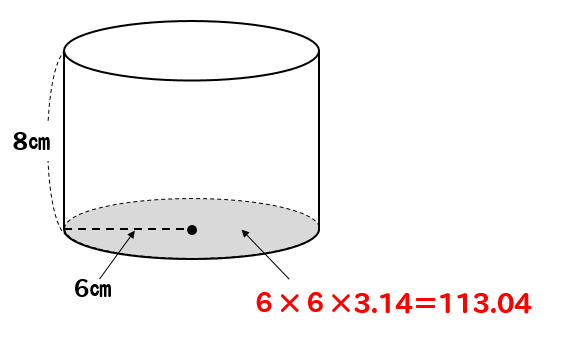
算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ
円柱 体積 計算 式
円柱 体積 計算 式-ρ=11×10 3 kg/m 3 Jx x軸に関する慣性モーメントkg·m 2 Jy y軸に関する慣性モーメントkg·m 2 Jx0 x0軸(重心を通る軸)に関する慣性モーメントkg·m 2 m 質量kgの関係を解(141′)式に代入して以下のように求められる. コンクリートで決まる場合 1 n c n S Nf x = 圧縮鉄筋で決まる場合 2 n rc nc S Nf nx d = − 解(147) 引張鉄筋で決まる場合 3 n t tn S Nf nD d x = −− 偏心軸方向力を受ける柱の許容軸方向力 N は,N1 ,N2 ,N3 のうち最小の値によって




角柱 円柱の表面積と体積の公式 数学fun
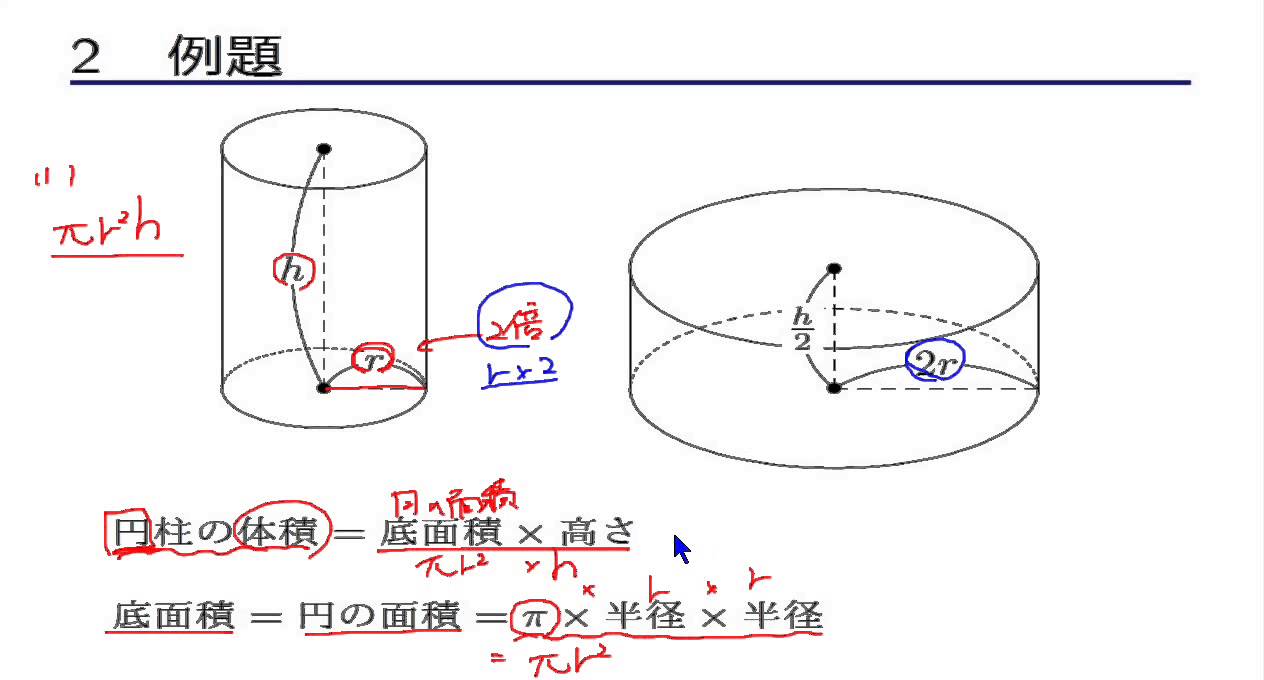
の計算方法の概要と計算例について説明する 2 理 論 計 算 式 21 熱応力の計算式 円柱鋼材の冷却過程の熱応力の計算式は,等 方性の無 限円柱鋼材で半径方向にのみ温度分布をもつと仮定すれ ば,原8)9)が導入している加熱過程の計算式がそのまま,レイノルズ数(レイノルズすう、英 Reynolds number 、Re)は流体力学において慣性力と粘性力との比で定義される無次元量である。 流れの中でのこれら2つの力の相対的な重要性を定量している。 概念は1851年にジョージ・ガブリエル・ストークスにより紹介されたが 、レイノルズ数はオズボーン · 円柱の体積の求め方はむちゃくちゃ簡単。 底面積×高さ っていう公式をつかえば、一発で体積を求めることができるんだ。 そんで、 底面積は、 半径×半径×円周率 だから、円周の体積はつぎの計算式で求められるよ。 半径×半径×円周率×高さ
一般の用法で 円柱 は、上記の意味での正円柱を有限の長さで切断し、両端が二つの円板によって閉じられているような図形を意味する。 もしらこの意味での円柱が 半径 r と長さ(あるいは高さ) h を持つならば、その 体積 V と表面積 S はエネルギー式 2 2 y T k y T v x T c p u 2 2 y T y T v x T u c p k 左辺 y T v y v x u T x T u y Tv x Tu x Tu よって、エネルギー式は、 2 2 y T x Tu柱の降伏曲げモーメント cMy計算に考慮する軸力倍率 cMyの計算は15技術基準 付1313~15式(ただし、同式中ag=2at、g=08とする)による。 柱頭部分の耐力は接続するはりの耐力も考慮し
· トップ 100 円柱 計算 式 各種断面形の軸のねじり 断面が円筒形型枠 P97 一次方程式 一次関数 三平方の定理ピタゴラスの定理 二次方程式 二次関数yax2 作図 円の性質 図形と相似 大地の変化 平方根 平面図形 式の計算 数学証明 文字式 植物の世界 標本調査区間における熱方程式については、既に「熱方程式に対する差分法i — 区間における熱方程式 —」である程度分かってきたと思う。 この文書では、円盤領域、扇形領域、円環領域、円柱領域、球領域などの「丸い」領域をターゲッ梁のたわみ計算、重量計算、エアー流量計算などが必要数値入力のみで算出できます。 らくちん設計 com ★重量計算★ -円柱- ★重量計算★
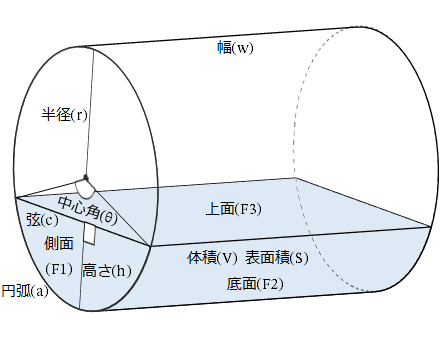



Excel関数 水平直円柱セグメントの体積や表面積を計算するhcylsegmentカスタムワークシート関数群 黒い箱の中
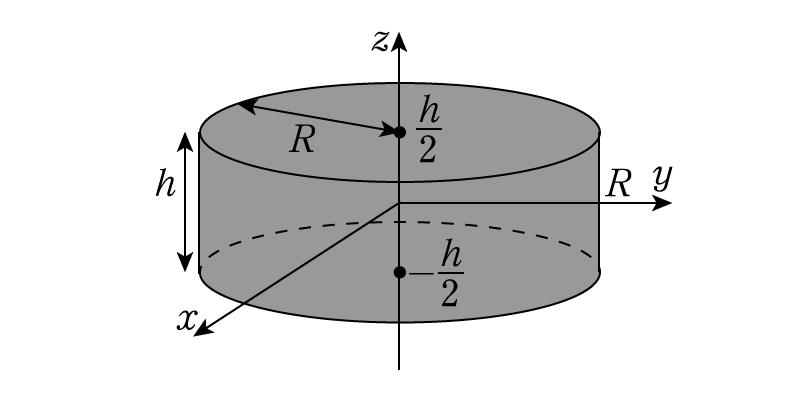



剛体の慣性モーメントの計算 物理の学校
円柱の体積を求める方法 円柱の体積を求める方法は とーーーーっても簡単です。 底面積×高さ これだけ! · 円柱・円筒の体積計算フォーム 円柱・円筒の直径cmと高さhcmから体積Vリットルを計算できます。 計算式 Vリットル=(π×r×r×h)/1000 ( ※1 半径r = 直径∅/2 ) ( ※2 cmで体積計算した場合、体積 Vを1/1000してリットル表記に変換 ) · 円柱の強制対流熱伝達率を計算する 流れに垂直に置かれた円柱の強制対流熱伝達率を計算します。 熱伝達率 h h は、ヌセルト数 N u N u と以下の関係にあります。 N u = hd λ N u = h d λ 強制対流における円柱の平均ヌセルト数は以下の実験式で計算できます



円柱を斜めに切断した時の切断された図形の体積の求め方は 底辺の円の直径15 Yahoo 知恵袋



1
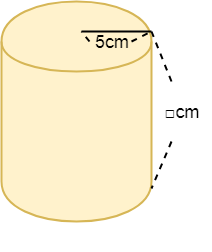
· これに丸棒(円柱)の長さ(奥行きL)をかけると丸棒の体積を計算できるのです。 つまり、丸棒の体積=πLA^2 /4と求められます。下の計算の係数が異なってくるので十分に注意して下さい。また、式(14)の中 のn とo は、接触の状態すなわちcos x によって決まる数です*。これを求める計 算は面倒なので、cos x からn とo を求める表または図ができていて、それによ り求めることができます。例題1 (23)式は、平行往復線路を形成する片側の直線導体1本、 l mの自己インダクタンス L の式である。この式を使用して、線路1kmあたりの自己インダクタンスmHを求める計算式を導け。ただし、対数は常用対数を使用するものとする。




算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ




円柱の内容積の求め方 あるテストの問題で 円柱の内容積を求めよとあ 数学 教えて Goo
· 計算手法上は上記のままでは new_value old_value の部分で桁落ちが心配されるため、 円柱座標での漸化式 † 円柱座標の場合、対応する停留条件は、注)式(711)のwoを gに、単位 を にtf/m 2 N/m2 浮力の作用領域 円柱部材に働く波力モリソン式 54 1 2 TD0024M uu D Du dF C D dz C d z D t S UU C D 9 8C M 9 9 /1 !1 # 23 & $1 dz dF T D u z x 7 •小口径部材に適用する •抗力項と慣性項の和で求める円柱の方程式は, (は任意) で表される。 媒介変数表示すると, , である。 切り開いて側面を考えると,円周の が新たな平面における横軸と考えることになる。 ところで,切断面の平面の方程式は,底面とαの角度で切断した場合, となるため, に, を




スタディピア 立体の表面積
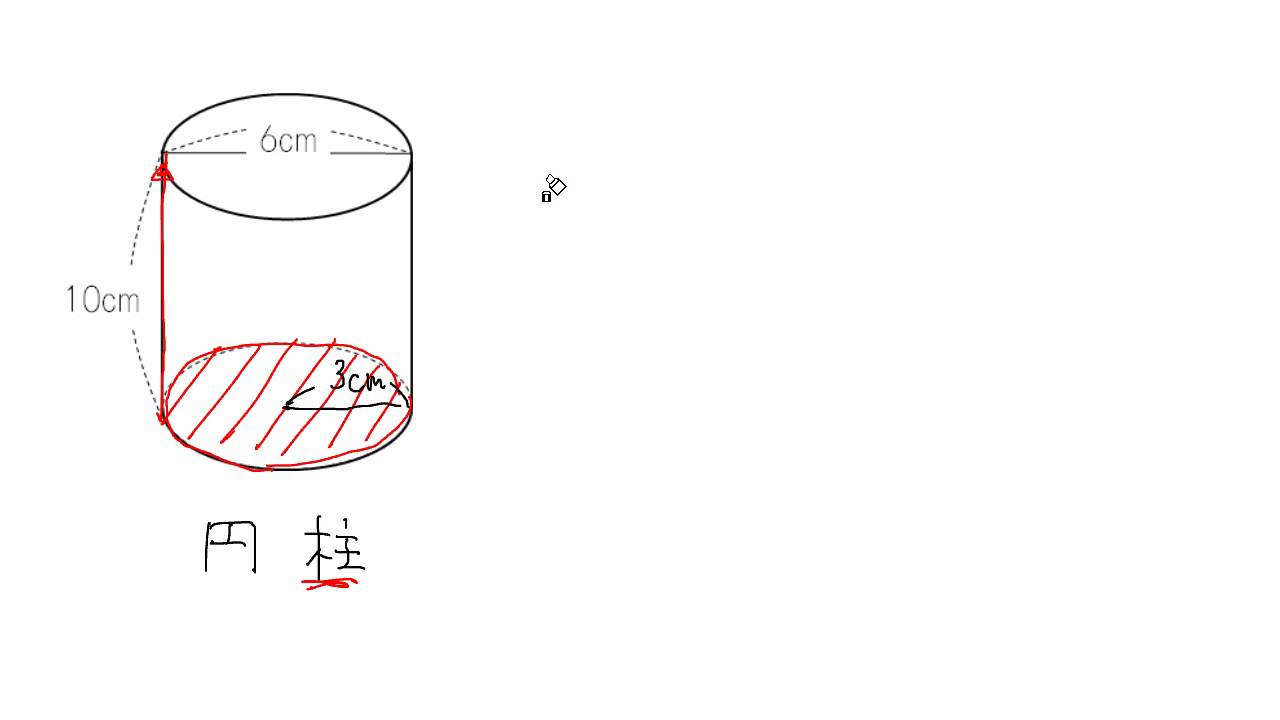



円柱の体積 Youtube
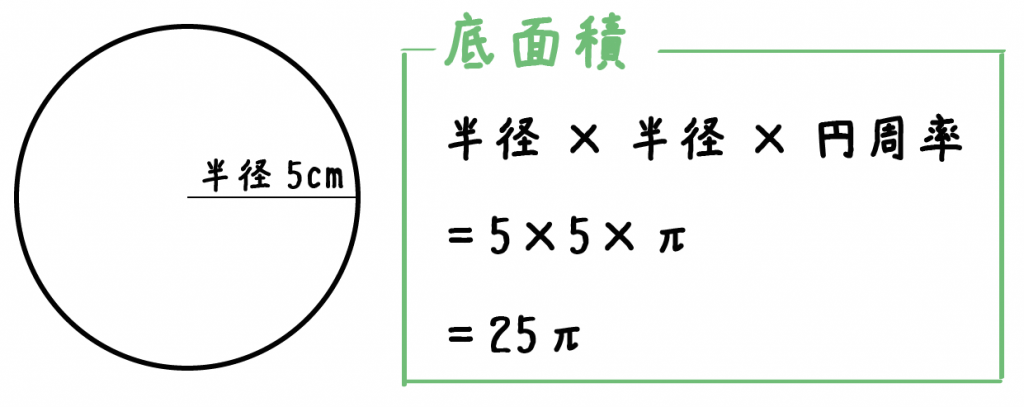
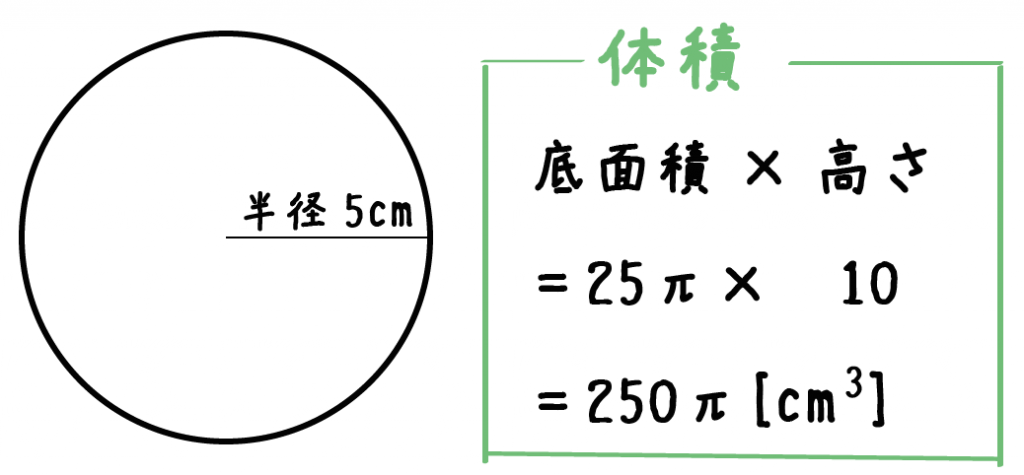
Dv計算の問題 ある座標系を他の座標系へ変換するときに関数行列式をいうのを用います。 この時の関数行列式をヤコビアンと呼びます。 このヤコビアンを使って実際にデカルト座標系から極座標、さらには円柱座標系への変換を、偏微分や行列計算を円の断面積は、 半径×半径×円周率 で計算します。 円周率は、概ね314程度です。 下図を見てください。 円と半径の距離を示しました。 下図の半径が5cmなので、断面積は 5cm×5cm×314=785c㎡ です。 · この公式は、これまでに説明してきた求め方にしたがうことで簡単に導くことができます。 (底面の円の面積)=(半径)×(半径)×(円周率)=r × r × π= πr 2 (円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h 円柱の体積を求めるには、与えられた半径や高さをこの公式に代入すればよいのです。 上の基本問題をこの公式を使って求める (1) r=5、h



1



円柱の容積は 1分でわかる意味 求め方と式 表面積の計算 体積と直径の関係
Q2 計算式と計算解 円筒の径方向の熱抵抗Rは次式で表されます。 ここにD 1 は円筒の内径、D 2 は円筒の外径、Lは円筒の長さ、 kは円筒材料の熱伝導率です。 ここでは円筒の内面と外面間の熱抵抗Rを用いて、オームの法則により温度差を計算することができます。 →Q2に戻る(円柱の表面積)= 2×(円周率)×(底面の円の半径)×{(底面の円の半径)(高さ)} 円柱の表面積を求めるには、この公式に底面の半径 r と高さ h を代入すればよいだけです。したがって、式(19)に式(18)を代入すると、ξηζ座標系とxyz座標系の応力成分の関係が 導かれ、これは応力の座標変換式に対応する。例えば、σξ,τξηは σξ=l1 2σ x+m1 2σ y+n1 2σ z+2(l1m1τxy+m1n1τyz+n1l1τzx)



円柱の体積の求め方 公式 小学生 中学生の勉強
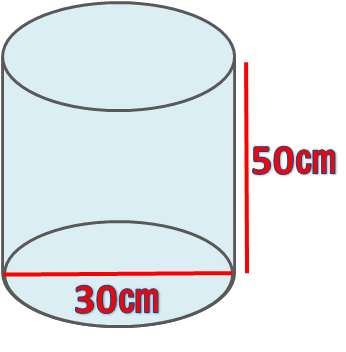



世界一分かりやすい 水槽の水量の計算方法 電卓でサクッ 水槽レンタル神奈川 マリブ 海水専門 メンテナンス
灰色セル:入力の必要はありません。精度良く計算させたい場合入力してくだ さい。 上記以外:備考以外は入力しないようにしてください。計算式が入力されてい ます。 凹円柱面 平面 凸円柱面 円柱緒元 面圧比較 数値 単位 備考 寸法緒元 凹面 平面 凸面円柱の体積を求める公式は 半径×半径×円周率×高さ です。 円の面積が 半径×半径×円周率 なので、 円の面積×高さ とも言えます。 円柱の体積を求める公式ントおよびピッチングモーメントが作用する。ここで、保護管の場合には一端支持の円柱に限 定されるため、前者の3 つの力のうち二つを考えれば良く、モーメントは無視できる。それぞ れの力は流体の密度と速度に比例する計算式で与えられる。ここで




角柱 円柱の表面積と体積の公式 数学fun



計算式の質問です 円柱の体積を求めたいのですが どのような計算式に Yahoo 知恵袋
上式の定積分の計算は、置換積分を用いてもいいが、軽妙に「四分円の面積」から求め る方が多数だろう。 また、この楕円は、半径 倍縮小して得られるという性質を用い て、 πa 2 としても得られる。具体例で学ぶ数学 > 図形 > 円柱の表面積と体積を求める公式 最終更新日 円柱の体積 V は、 円周率× 半径 × 半径 × 高さ 円柱の表面積 S は 2 ×円周率× 半径 × 半径 + 2 ×円周率× 半径 × 高さ このページでは、円柱の表面積について詳しく説明(1318)式、 (1319)式に(1336)式、 (1337)式を代入すると となります。半径rの点の半径方向変位uは、(1316)式に(1338)式、 (1339)式を代入して得られます。 内圧を受ける円筒の応力と変形の計算例




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




基礎編 1 2 径方向熱伝導 理論式 熱設計トレーニング 流体シミュレーション Flowdesignerのアドバンスドナレッジ研究所 Akl
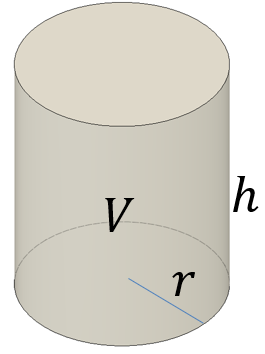
底面の半径が $10\\mathrm{cm}$、高さが $15\\mathrm{cm}$ である円柱の容器に水を満タンに入れた。水は何リットルか? 解答 円柱の体積は (半径)×(半径)×(円周率)×(高さ) なので、 $10\times 10\times \pi\times 15=1500\pi\\mathrm{cm}^3$ よって、水の量は $1500\pi\div 1000$ $=15\pi$円柱の体積を求める公式は、次の通りです。 V = Sh = πr2h V = S h = π r 2 h ここで、V は円柱の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の円の半径です。なお,円管の温度分布は,円柱座標(r:半径,I:角度,z:長さ)を用いれば,次の熱伝導の基礎式に従うものとする。 ここで,Uは密度,Cp は定圧比熱,t は時間,qv は単位体積当たり単位時間に発生する熱量である。(H15) p qv z T z T r r T r t r r T C ¸¸ ¹




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学
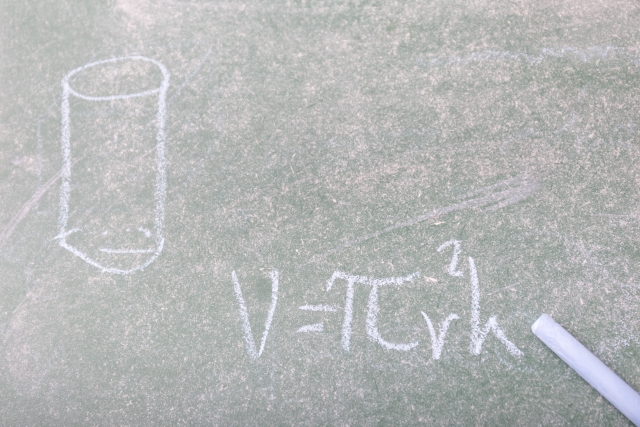



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
数式で計算する場合は、半径をr・高さをh・円周率をπとすると、 (r 2 ×π×2)(2×r×π×h) となり、まとめた式にすると 2πr(rh) となります。この式に数値を当てはめれば円柱の面積を計算できます。 円柱の表面積を求める公式 · 簡単公式五角形の内角の和を3秒で計算できる方法 中1数学 計算公式円錐の表面積の求め方がわかる3つのステップ 中1数学 一次方程式長椅子の文章問題の解き方がわかる3ステップ 中2数学




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Search Q E7 90 81 Ae E4 93 E7 8d Tbm Isch




円柱の体積の求め方 公式と計算例




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく
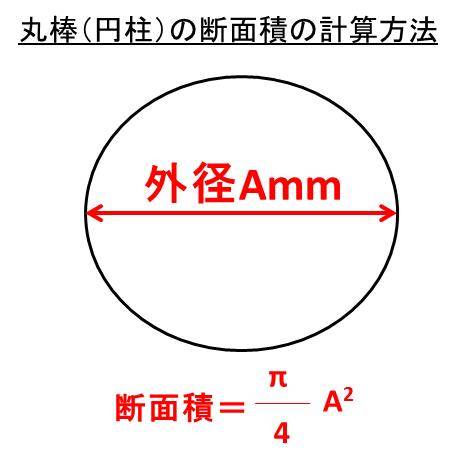



鉄やステンレスの円柱の重量計算 丸棒の重さ 質量 の求め方 モッカイ
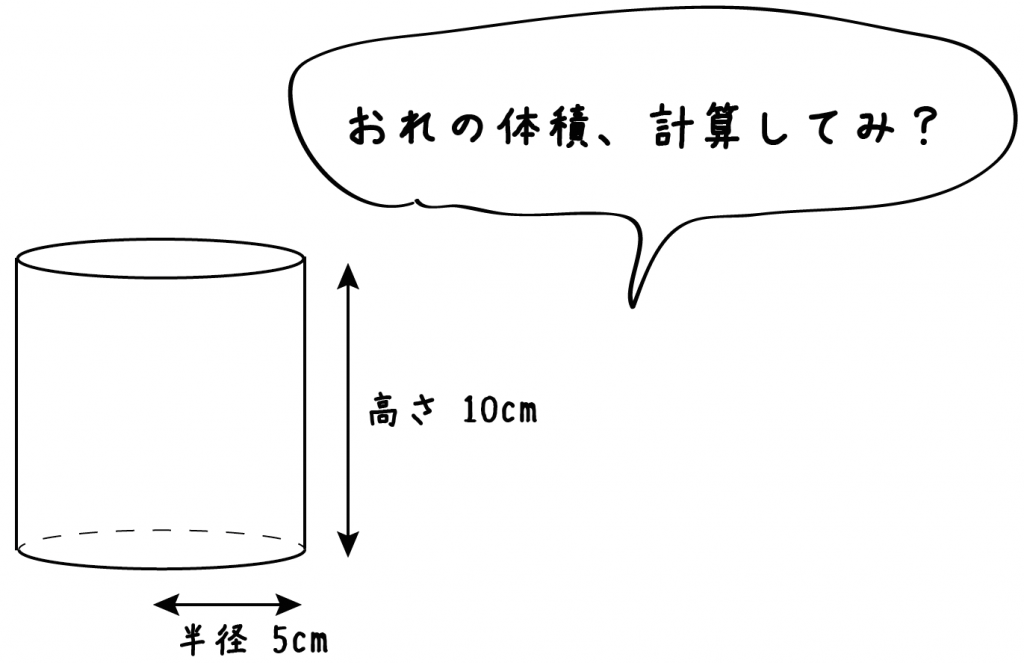



計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




M Sudo S Room 実用性の高い計算式 円柱斜切断体の体積



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典



円筒の体積計算 デジタル教科書 電子教科書



丸棒 円筒のねじり計算
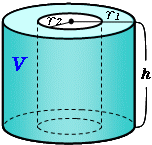



中空円柱の体積 高精度計算サイト




小6 算数 小6 26 角柱と円柱の体積 基本編 Youtube
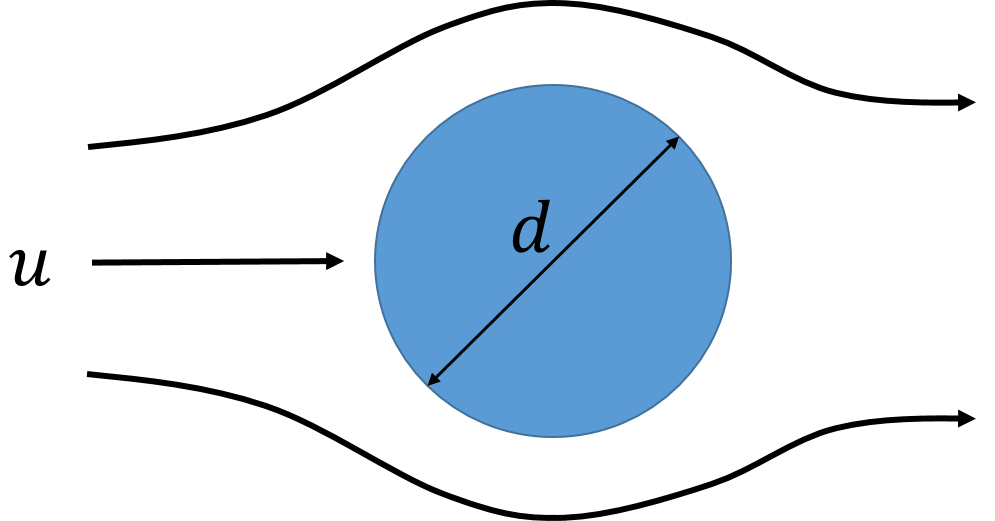



円柱の熱伝達率の計算 強制対流熱伝達 科学技術計算ツール




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




M Sudo S Room 実用性の高い計算式 円柱斜切断体の体積



ヘルツ接触 円柱面 円柱面 線接触




丸棒の重量 円柱の体積と重量の求め方 鉄の場合




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




基礎編 1 2 径方向熱伝導 理論式 熱設計トレーニング 流体シミュレーション Flowdesignerのアドバンスドナレッジ研究所 Akl




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



質量と比重
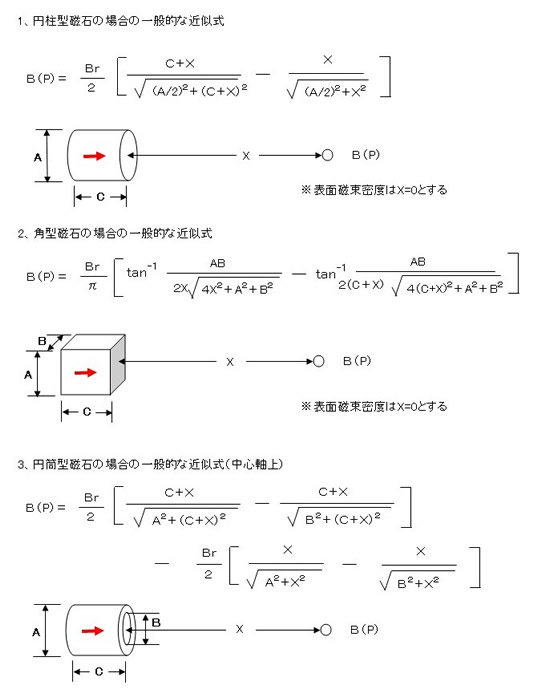



お客様サポート よくあるご質問一覧 neomagホームページの磁束密度と吸引力の計算式を教えてほしいのですが




P14 Descubre Como Resolverlo En Qanda



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典




この問題の答えって2prhですか どなたか教えてください 私が計算した式は Clear




空間図形 円柱の側面積の求め方がわかりません 中学数学 定期テスト対策サイト




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




角柱 円柱の表面積と体積の公式 数学fun
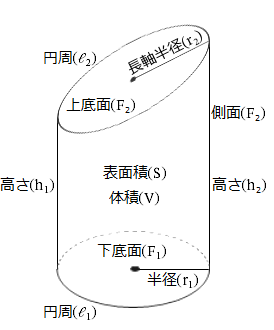



Excel関数 斜切直円柱の体積や表面積を計算するtrunrccylinderカスタムワークシート関数群 黒い箱の中




円柱の表面積と体積を求める公式 具体例で学ぶ数学




面積 体積 計算ツール 福井鋲螺株式会社 冷間鍛造 冷間圧造 ヘッダー加工の専門メーカー リベット 特殊形状パーツおよび省力機器の製造 販売




表面積の求め方 計算公式一覧




円柱の表面積と体積を求める公式 具体例で学ぶ数学
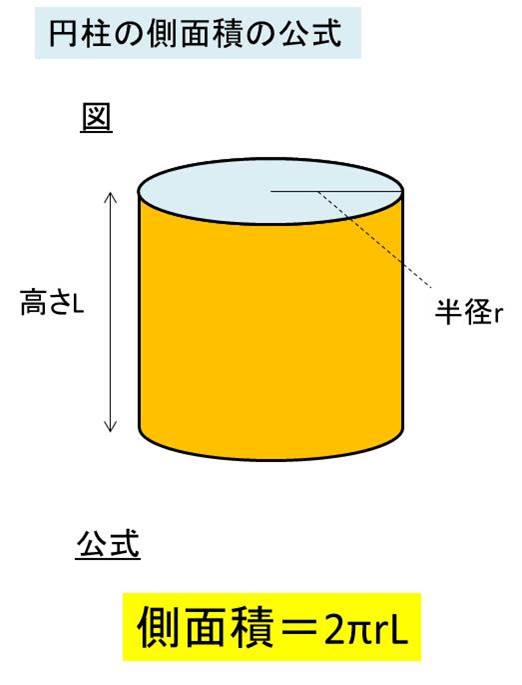



円柱の側面積 底面積 表面積を求める方法 モッカイ
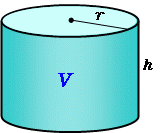



直円柱の体積 高精度計算サイト
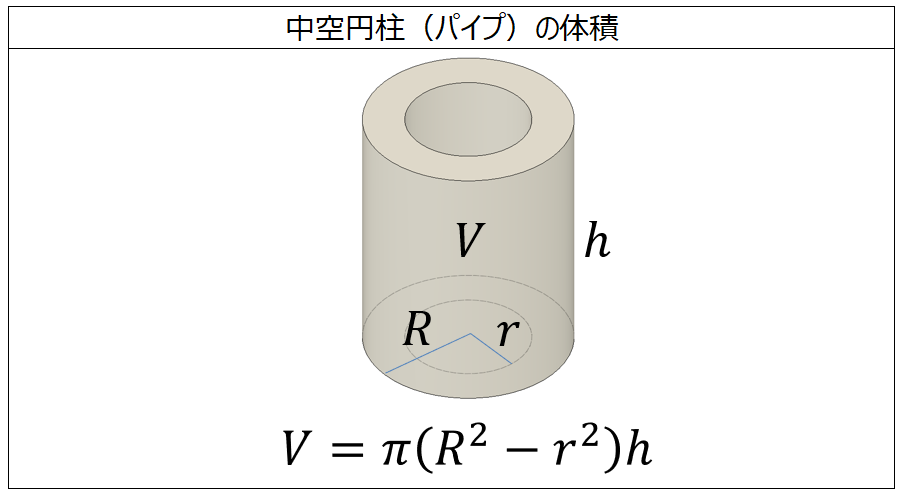



体積の計算 中空円柱 パイプ 製品設計知識
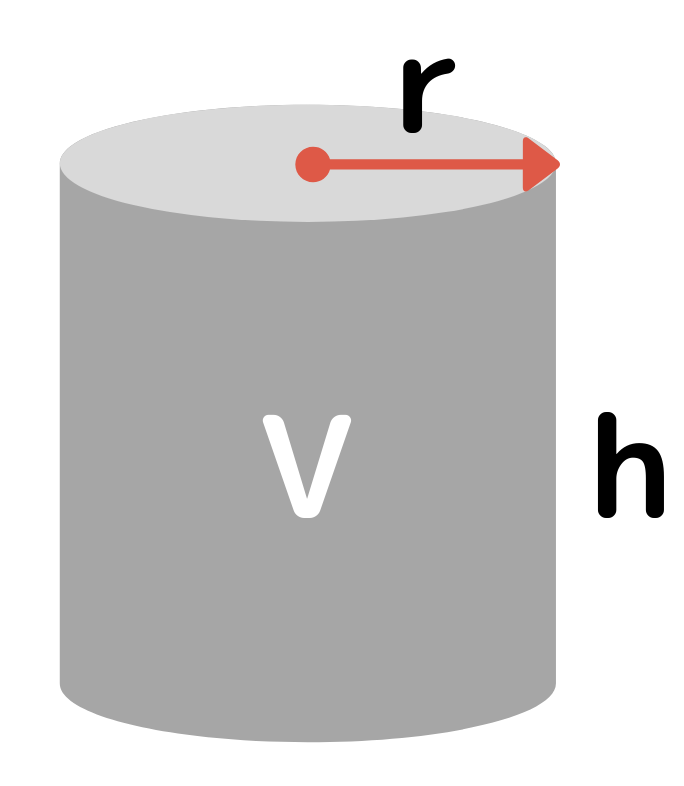



円柱の体積の計算フォーム 直径 高さ Cm 体積 リットル を算出 寝袋 シュラフのプロが極秘で教える 失敗しない選び方 使い方




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ



1




円柱の体積の計算 リットルへの変換も考えてみよう 中学数学 理科の学習まとめサイト




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学
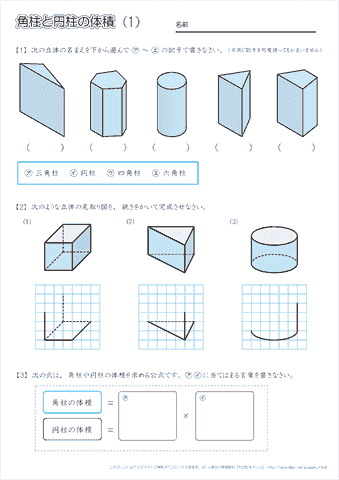



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




簡単 円柱の体積公式は底面積 高さ 必ず解きたい計算問題付き 高校生向け受験応援メディア 受験のミカタ




円の面積 円柱の体積と比重 日々自己の鍛練




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
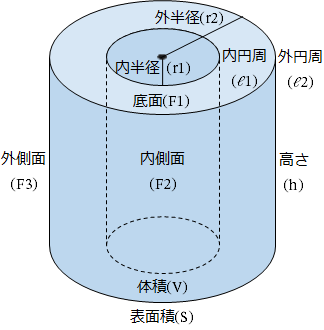



Excel関数 中空直円柱の体積や表面積を計算するrcholcylinderカスタムワークシート関数群 黒い箱の中



ヘルツ面圧計算 簡易版 取扱説明書 ヘルツ面圧計算 簡易版 取扱説明 Manualzz




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun
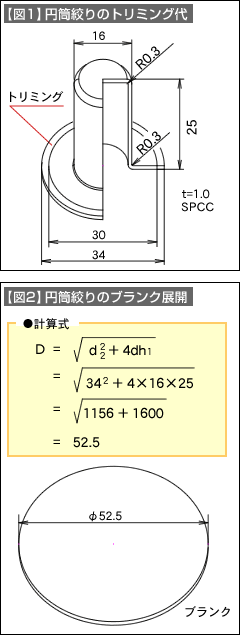



円筒絞りのブランク展開 円筒絞りの工程設計 円筒絞りの工程設計 その2 技術情報 Misumi Vona ミスミ
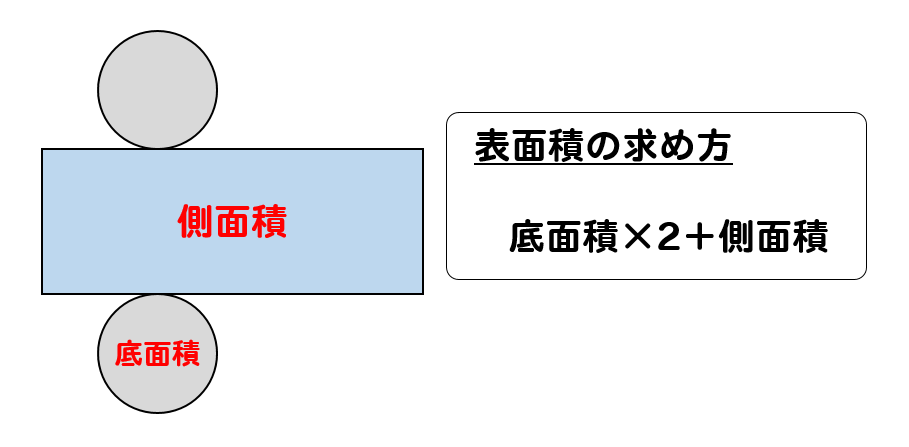



円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ
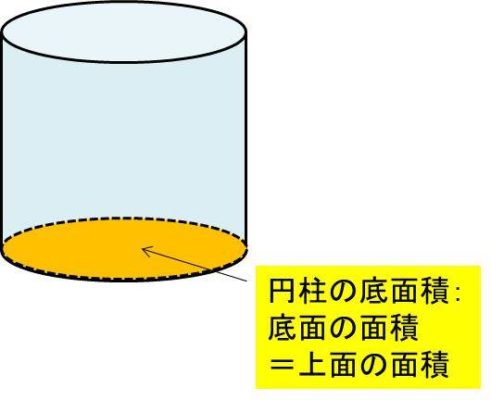



円柱の側面積 底面積 表面積を求める方法 モッカイ
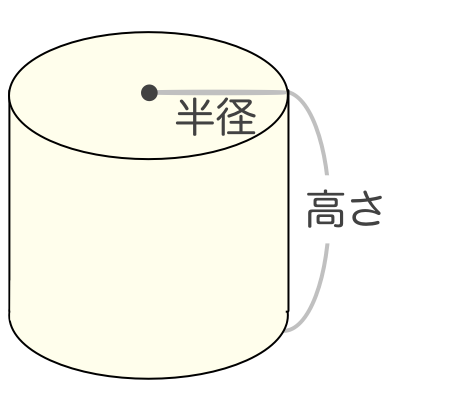



円柱の体積 簡単に計算できる電卓サイト




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典




P14 Descubre Como Resolverlo En Qanda




円柱の体積の求め方 公式 小学生 中学生の勉強




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




円柱の体積の求め方 公式 小学生 中学生の勉強
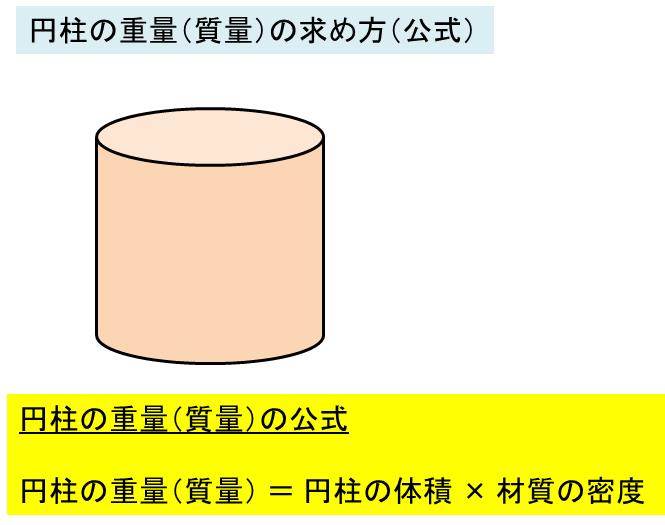



丸棒の重量 円柱の体積と重量の求め方 鉄の場合




円柱の表面積 Youtube
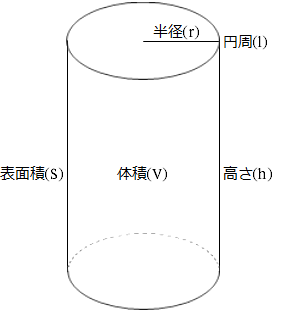



Excel関数 直円柱の体積や表面積を計算するrccylinderカスタムワークシート関数群 黒い箱の中



断面積とは 1分でわかる求め方 長方形と円の公式 単位 計算方法 直径との関係




円柱の水槽に球を入れる問題 苦手な数学を簡単に




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
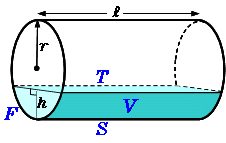



一部が欠けた直円柱の体積 高精度計算サイト




円柱の表面積の求め方 公式と計算例
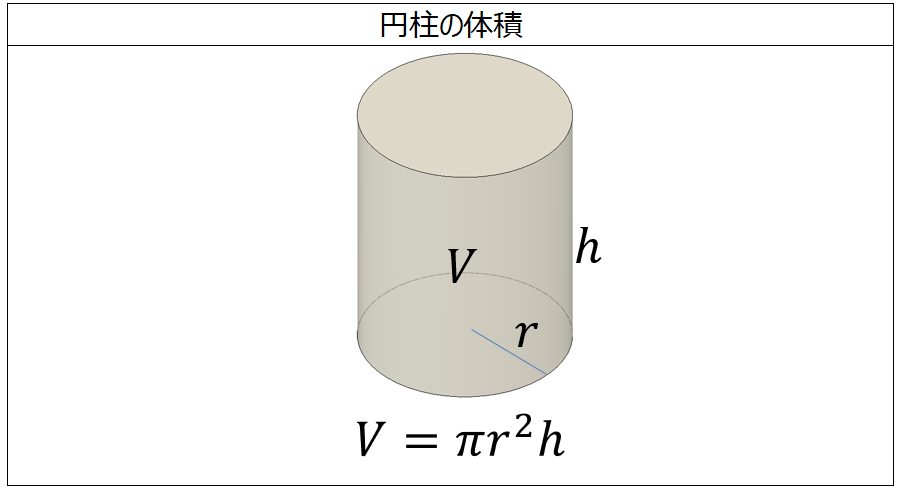



体積の計算 円柱 製品設計知識



円柱導体の高周波インピーダンス 表皮効果含む の計算 高精度計算サイト




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun



計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円柱の表面積の求め方 公式と計算例



円柱の側面積は 1分でわかる求め方 公式 底面積と表面積 体積との関係



U9j580gf8iba369ji2w Xyz P 296




算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円柱の容積は 1分でわかる意味 求め方と式 表面積の計算 体積と直径の関係



計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中2数学 式の計算 3 1 文字式の利用 Youtube




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



体積の計算 円柱 製品設計知識




慣性モーメントj Kg M 2 の計算式 技術資料 オリエンタルモーター株式会社




円柱の体積 表面積 側面積 計算機 かんたん計算機




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun



0 件のコメント:
コメントを投稿