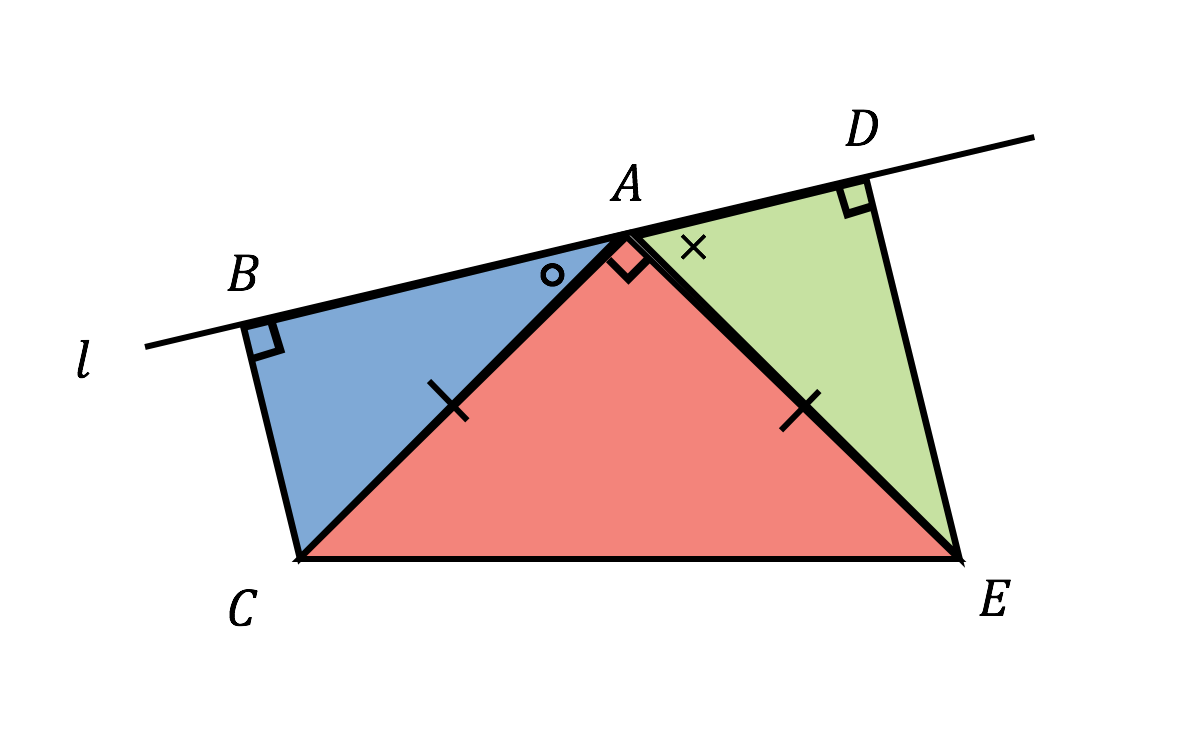
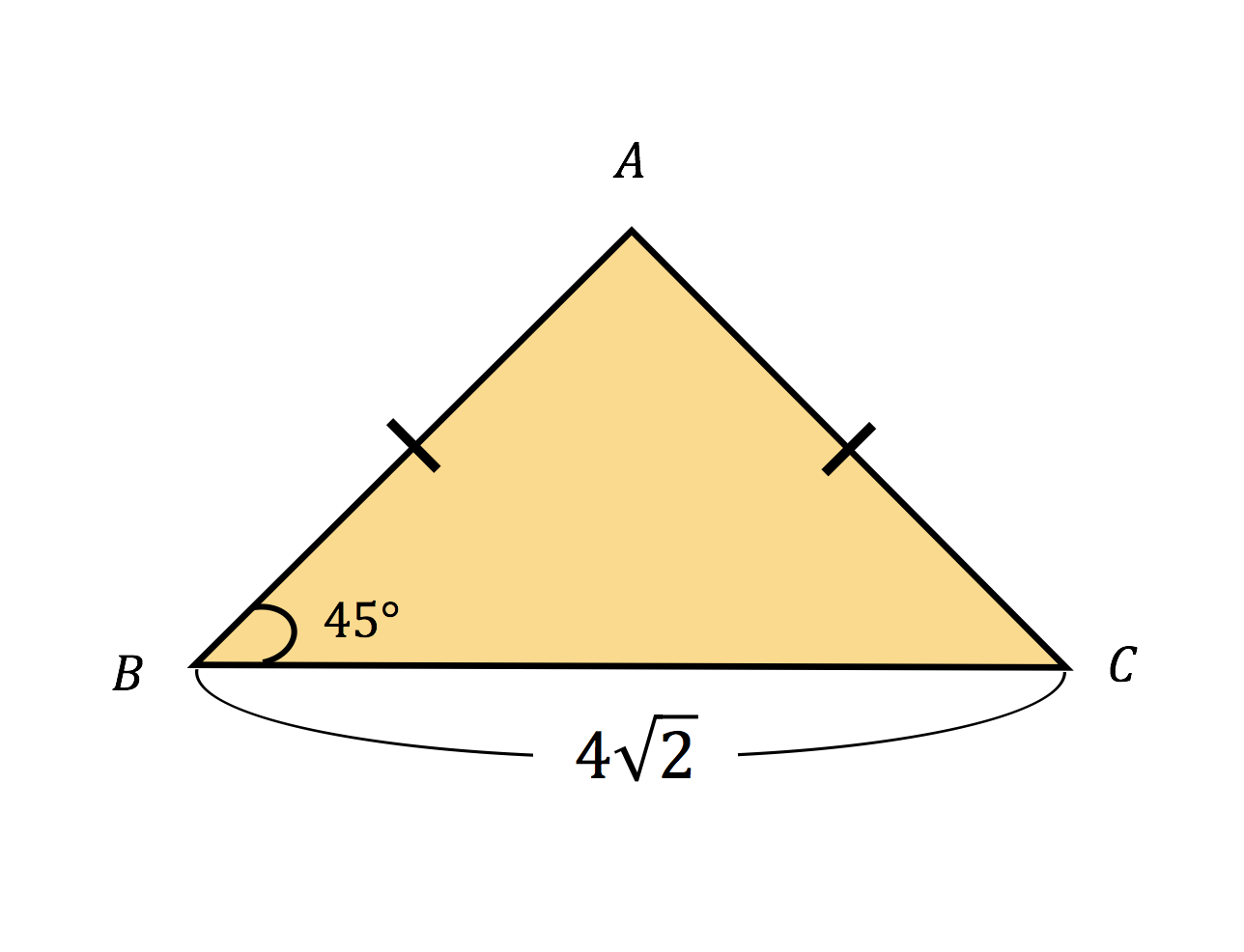
三角形の頂点数と画質との関係を明らかにしていくための助走的な研究として圧縮された画像内の屓点数を効率よく求 めるアルゴリズムを提案する キーワード 直角二等辺三角形の二等分割, 二分木,組合せアルゴリズム, 画像処理 1 まえがき 近年,実は、先ほどの例題の三角形と同じ三角形です。 なので、 BC を斜辺とする直角二等辺三角形です。 ABACBC=11\sqrt { 2 } を使って、 AB=AC=4 がわかります。 よって、先ほどの面積の公式 \displaystyle \frac { 1 } { 2 }a^2 を使って、 \displaystyle \frac { 1 } { 2 }×4^2=\style { colorred;中点連結定理、直角、二等辺三角形を利用した問題は、 5月の記事「 少しずつ消化して 」で紹介したように、 今春の大阪府公立入試一般選抜のB問題で出題されました。 「 少しずつ消化して 」の問題は円や三平方の定理が絡んでいて 範囲外なのでやら
3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ
直角 二 等辺 三角形 定理
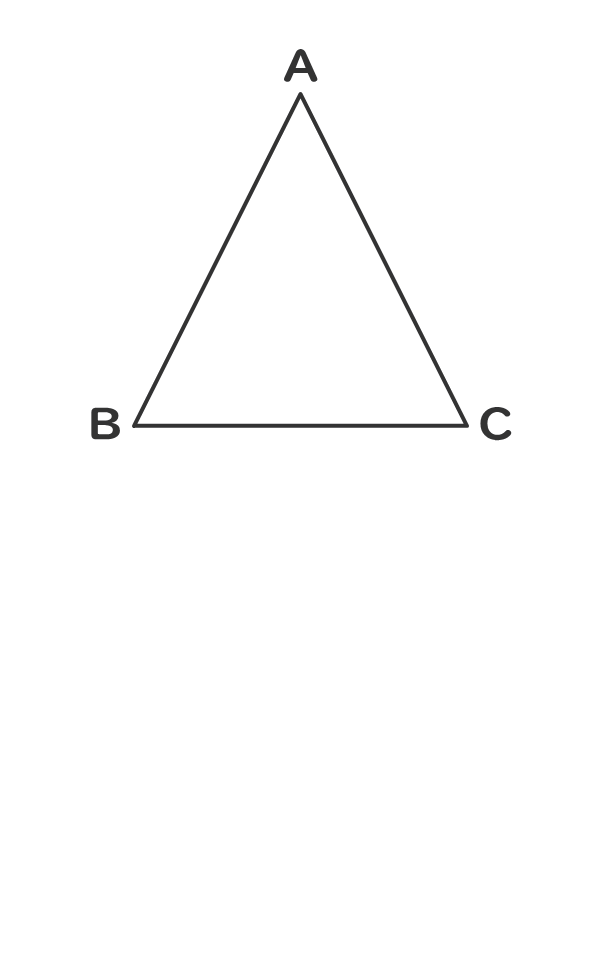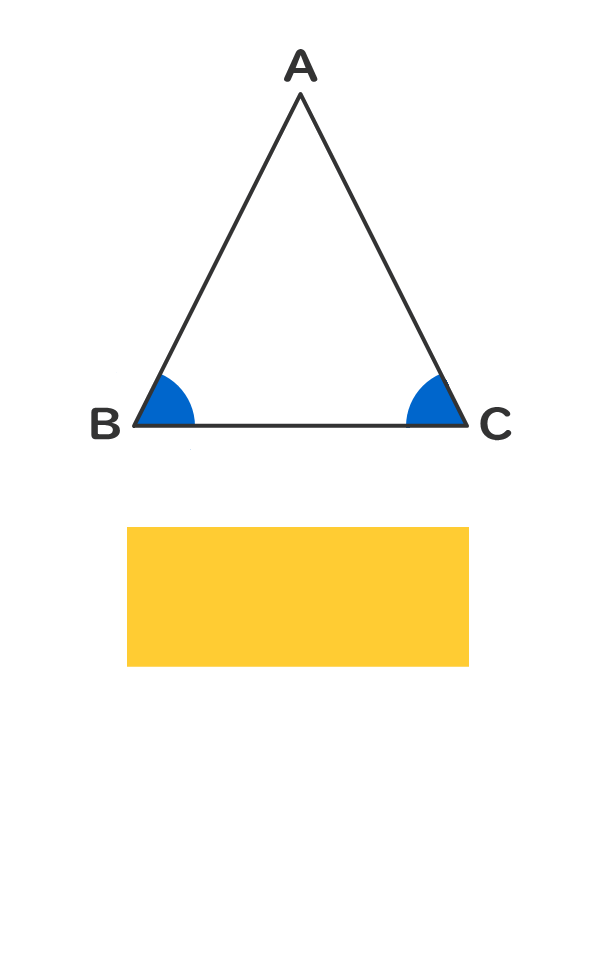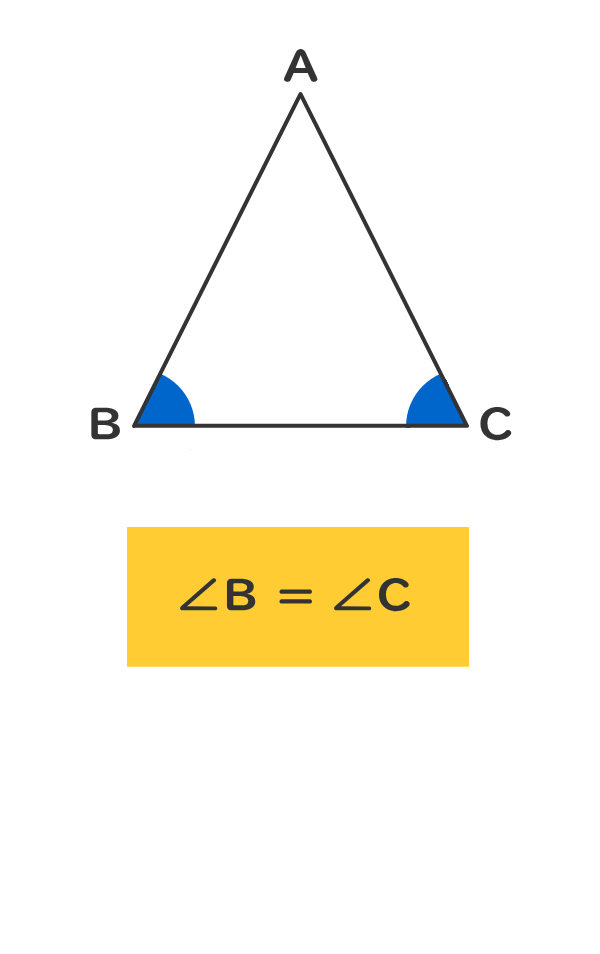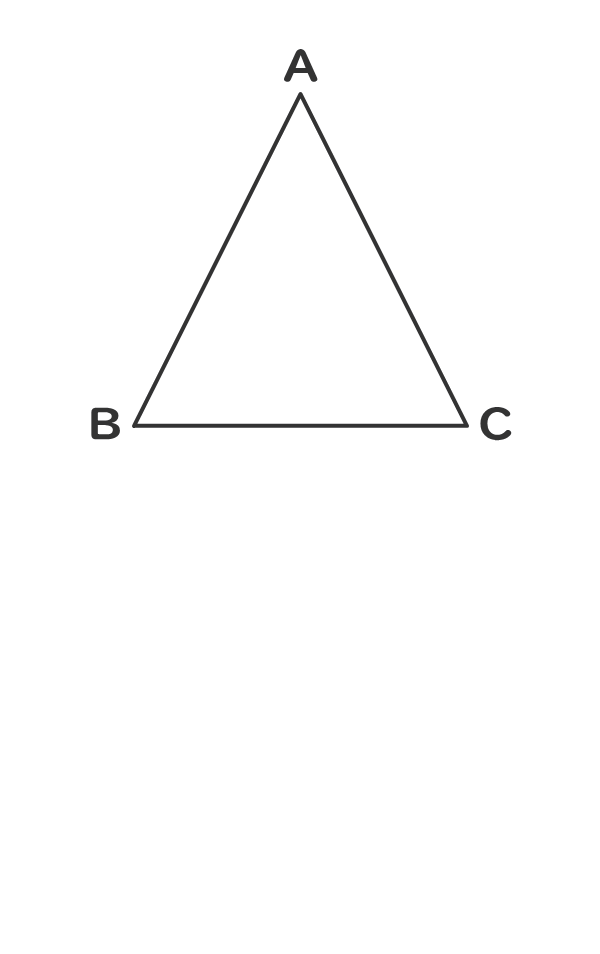
直角 二 等辺 三角形 定理-同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し い。 錯角 が等しければ、2直線は平行 三角形 四角形定理:二等辺三角形の底角は等しい この定理を当然のこととして知っている人も多いと思います。図でも確認しておきましょう。 どこ ダダオ・シャオムの A Piece of Paper HOME ABOUT STUDY CONTACT 数学学習の段階番外編:二等辺三角形の底角の定理 どうもシャオムです。 これまで3回




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
二等辺三角形は、 = となる三角形のことであり、 を頂角、, を底角という。 定理 113 二等辺三角形の底角は等しい。 証明 二等辺三角形を (=) とおこう。このとき、bc の中点を x とおく。さて、赤い部分が二等辺直角三角形になるのはなぜ? 教員採用試験の問題集にあり、恥ずかしながら自分にはわからなかったので質問です。 正方形の中に、正三角形が図のように内接しているとします。 そのとき、赤い三二等辺三角形と定理・定義 ab=acの二等辺三角形で、bd=ceとすれば、∠ade=∠aedであることを証明しなさい。という問題で、 abdと aceの合同を示し、対応する辺が等しいことからad=ae。 adeは二等辺三角形だから 三平方の定理の公式で、直角二等辺三角形は1
中学数学(三平方の定理):直角二等辺三角形 数学(中学) 対象 高校生 再生時間 327 説明文・要約 ※ よく出てくる特別な三角形なので、 30°・60°・90°の直角三角形 と併せて覚えておいてください ・直角二等辺三角形(45°・45°・90A三平方の定理(ピタゴラスの定理) 直角三角形の直角をはさむ2 辺の長さをa,bとし,斜辺の 長さをcとすると a2 +b2 =c2 が成り立つ。これを三平方の定理(ピタゴラスの定理)という。 直角三角形の直角二等辺三角形から成る多面体的アニュラスは2つの3辺形(正三角形)を境 界としてもつ鏡像の関係にある2つの多面体的アニュラスだけが存在する 私たちは,(a) の等角等辺2n 辺形から得られる2n の直角二等辺三角形から成 る多面体的アニュラスがリバーシブルかどうかを調べた. 定理 n を
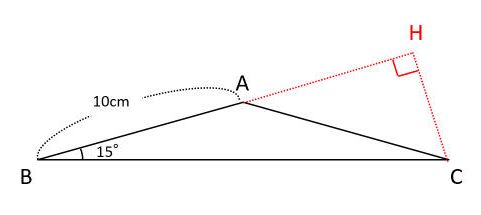
MF=CFの直角二等辺三角形になる。 MFCFMC=11 2, MC=6cmより MF=CF=3 2 また、BC=12 2 cm BE=x なので EF=12 23 2x =9 2x 直角三角形MEFで三平方の定理に当てはめると (3 2) 2 (9 2x) 2 = x 2 2 xx 2 =x 2 18 2 x = 180 x=5 2直角二等辺三角形の選択入力値から他の要素の値を計算します。 h = a 2 b = a √ 2 L = ( 1 √ 2 ) a S = a 2 4 h = a 2 b = a 2 L = ( 1 2 ) a S = a 2 4 入力指定直角二等辺三角形とは、 二等辺三角形の特徴と直角三角形の特徴をあわせもった三角形 のことです。 直角二等辺三角形の定義 \(3\) つの角のうち、\(2\) つの角がそれぞれ \(45^\circ\) である三角形を「直角二等辺三角形」という。




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
5 2 直角三角形,鋭角三角形,鈍角三角形であるための条件 21 余弦定理 abc の1 つの角と3 つの長さの間に次の等式が成り立つ.この等式は余弦定理 と呼ばれる.余弦定理は 「2 辺の長さと夾角(隣り合う2 辺のつくる角) がわかれば,三角定規には、\(\boldsymbol{45^{\circ}}\) の角を持つ直角二等辺三角形と、\(\boldsymbol{30^{\circ},\;60^{\circ}}\) の角を持つ直角三角形の \(2\) 種類があり、それぞれ 特別な \(\boldsymbol{3}\) 辺の長さの比 を持ちます。二等辺三角形の性質 定理① 二等辺三角形の底角は等しい。 定理② 二等辺三角形の頂点の二等分線は、底辺を直角に2等分する。 正三角形3辺が等しい三角形(定義) 二等辺三角形と正三角形 46°




この図形は底面が直角二等辺三角形ab Ac 4cm Ad 6cmの三角柱です Clear




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su
このとき, b c bc bc と e f ef ef をくっつけてできる三角形 a c d acd a c d は二等辺三角形となる。 よって, ∠ C A D = ∠ C D A \angle CAD =\angle CDA ∠ C A D = ∠ C D A であり,2つの直角三角形は斜辺と1つの直角でない角が等しい。2 が当てはまる、 底辺 と 高さ を探す ほうが、簡単だと思います。 直角二等辺三角形の重なってるところの面積の求め方を教えてください斜線の引いてある直角二等辺三角形だと この公式。 と 別々に覚えるよりも 、シンプルに、 (底辺) ×




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ
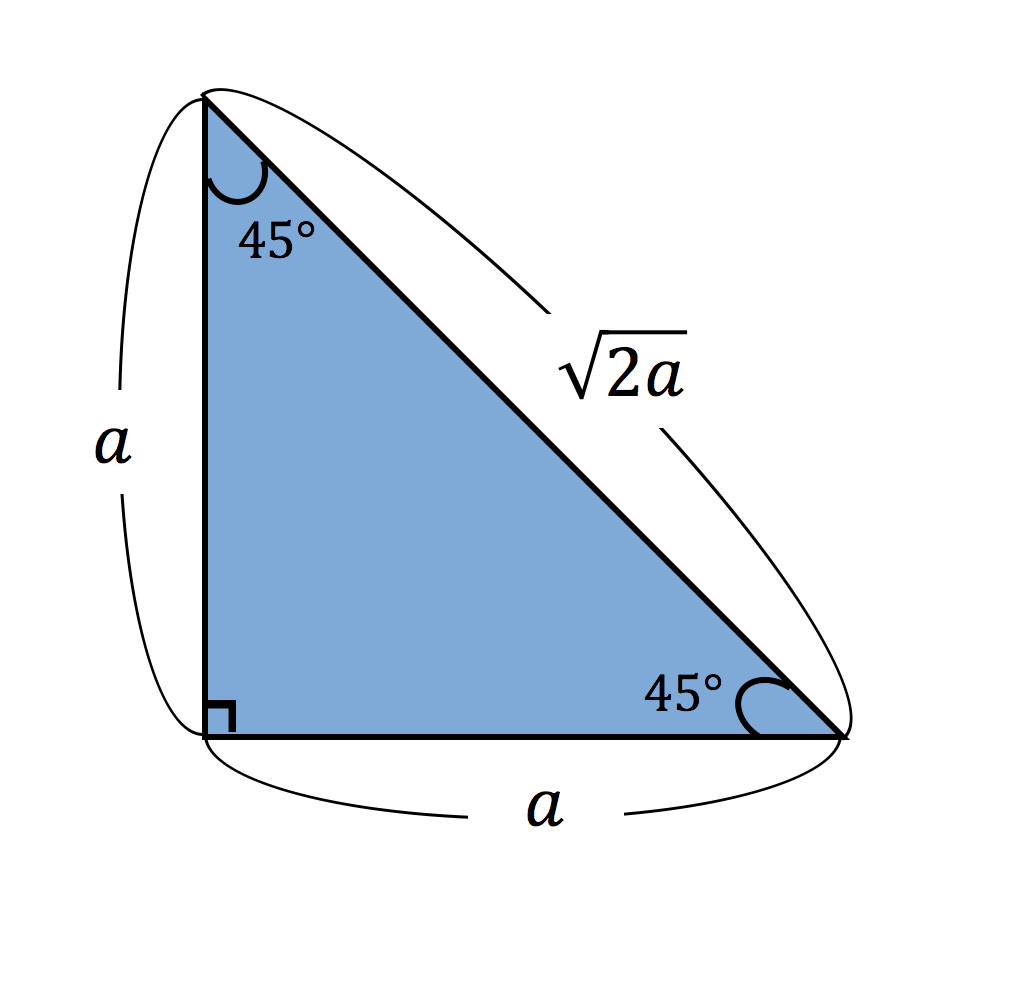
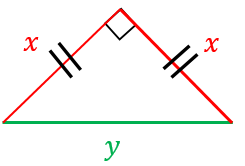
直角二等辺三角形の辺の比は「三平方の定理」から導くことができます。 直角二等辺三角形の底辺と高さの長さは同じです。 底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。 よって、直角二等辺三角形の辺の比は「1:1;√2」です。 今回は、直角二等辺三角形と三平方の定理との各辺の比が決まった三角形がある 三角形の中でも、各辺の比率が決まっている三角形が存在します。 これらの三角形は、図形を学習していく上で特に重要なので、この機会に覚えてしまいましょう。 直角と45°の組合せ まず、次の図のような直角二等辺三角形ですです。これは直角二等辺三角形の場合の三平方の定理ですね! やはり、ピタゴラスは只者ではありません。 ちなみに、上のタイルを一般の直角三角形に応用した図は です。ここで面積が 大きな正方形=小さな正方形+直角三角形×4




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




直角三角形の合同条件とその証明 数学fun
今、二等辺三角形が熱い! ~小学校の算数が懐かしい デイリーポータルZ 21年5月31日 自分が小学生時代に流行ったマンガやアニメ、おもちゃなどに触れると、懐かしむのみならず改めてハマってしまうことはないだろうか。 筆者は最近、で中学二定点を頂点とする二等辺三角形・直角三角形の第三の頂点 本記事では、二定点を頂点とする 二等辺三角形 ・直角三角形の第三の頂点の存在範囲について考えます。 二つの定点はそれぞれA,Bと定めます。 当然のことながら、三角形ができなくなるような直線AB上の点は最初から除外し正三角形・二等辺三角形・直角三角形の書き方(作図)まとめ! 直角三角形の定理(三平方の定理) 直角三角形では、辺の長さに関する 三平方の定理 が成り立ちます。



三角形の種類を判定しよう 電験3種web



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ
次に、直線 AC A C 上に、 CD = a C D = a となるような D D を下図のようにとる。 このとき、 BCD B C D は直角二等辺三角形となる。 さらに、下図のように、直線 DB D B と円 O O の B B ではない交点を E E とし、さらに直線 AE A E と直線 BC B C の交点を F F とする。 このとき、 ∠BEF = 90∘ ∠ B E F = 90 ∘ であり、対頂角から ∠BEF = 45∘ ∠ B E F = 45 ∘ なので、 BEF B E F も上の二つの結果より,三角形 d e b deb d eb と d f c dfc d fc は合同(直角三角形において斜辺と他の一辺がそれぞれ等しい)。 よって E B = F C EB=FC EB = FC 以上により A B = A E E B = A F F C = A C AB=AEEB=AFFC=AC A B = A E EB = A F FC = A C図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 °




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube
A=b など a=b の→二等辺三角形 a 2 =b 2 c 2 など→ ∠A=90°} { 8 } が求める面積になります。 この公式を必ずしも使う必要はありませんが、覚えておくと三角形の形状問題(正三角形,二等辺三角形,直角三角形など三角形の種類を言い当てる問題)や証明問題においては,正弦定理や余弦定理を変形して,角度に関する式を辺に関する式に直してから考えるのが原則です. ・ tan A は上記2つを用いてとします
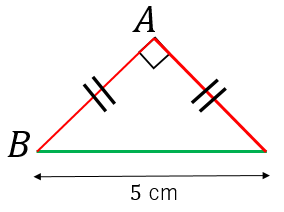



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



1
No06 モーリーの定理 問題 右図において、 abc は直角二等辺三角形とする。この とき、各頂点の角を3 等分する2 直線をひき、隣り合う2 つずつの交点をそれぞれ点D,E,Fとおく。このとき def は正三角形となることを確かめよ。 考え方 正確に図をかいて角度をはかれば、正三角形となることが(6) (7) (8) (9) (10) (11) (12) ab=ac ad=cd ab=ac cd=ce a b c d a b c d a b c d f eX = √2 になるぞ。 この直角二等辺三角形からピタゴラスは「無理数」を発見したと言われているんだ。



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
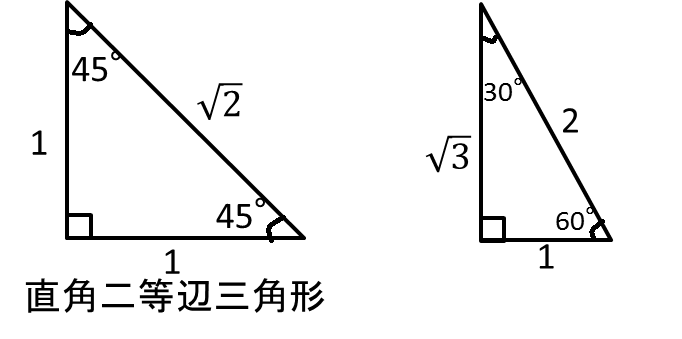



140字で高校受験 数学 三平方の定理 三平方の定理を習ったら 合わせて覚えておこう 三角定規 90 45 45 1 1 2 直角二等辺三角形 90 60 30 1 2 3 2が斜辺 T Co Uckznroe5w Twitter
直角二等辺三角形の「斜辺だけ」わかってる場合だ。 このとき、 残りの辺はつぎの公式で計算できるよ。 斜辺をb、等しい辺の長さをaとすると、 a = √2b /2 で求められるんだ。 たとえば、 斜辺が4cmの直角二等辺三角形DEFがいたとしよう。三角形と円 三角形と円 円周角と中心角 定理 1つの弧に対する円周角は常に一定で、その弧に対する中心角の に等し い。 点Pを何処にとっても ∠APBの大きさは変わらない。 円周角は常に中心角の半3年(平方を利用した積の計算の対戦ゲーム,三平方の定理の幾何的証明:初級パズル,三平方の定理の幾何的証明:中級パズル,直角二等辺三角形に近いピタゴラス数) 書誌 数学教育 19年4月号 著者 須田 学 ジャンル 算数・数学 本文抜粋 対象 中学3年 種別 特集 仕様 全6ページ (60ポイント



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典



1
平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい °




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



直角二等辺三角形と三平方の定理の関係は 3分でわかる計算 公式 辺の比 例題




2つの直角三角形の角の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




名門国立小のカリスマ先生に聞く なんでこれがわからないの でイラっときた時の教え方 Forbes Japan フォーブス ジャパン




三平方の定理の証明 外接円と直角二等辺三角形を利用した証明 Fukusukeの数学めも




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




高校数学 三角形の形状 正三角形 二等辺三角形 直角三角形 受験の月




三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語




3 4 5の三角形で 本当に直角ができる Note Board
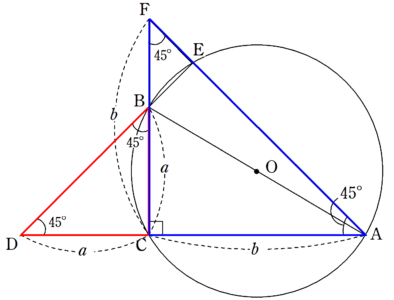



三平方の定理の証明 外接円と直角二等辺三角形を利用した証明 Fukusukeの数学めも




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係




直角二等辺三角形の書き方教えてください お願いします 直角二等 その他 悩み相談 人生相談 教えて Goo
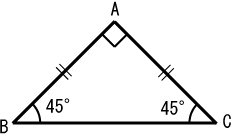



直角二等辺三角形 Wikipedia




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




数学デー 公式 本日は ベイズの定理について話したり キリンの画像で遊んだり フラクタル図形についての議論をしたりしました 直角二等辺三角形を螺旋状に並べると 最初の三角形の斜辺の長さがr r 7となり これが 2に等しいことからrを求め




世界に1ペアだけ 周りの長さも面積も同じ直角三角形 二等辺三角形 慶大院生ペア証明 朝日新聞デジタル




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学




各辺の比が決まっている三角形 中学数学 By Okボーイ マナペディア




数学 中2 64 二等辺三角形 Youtube




二等辺三角形になることの証明 Youtube




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




無料印刷可能直角二等辺三角形 比率 最高のぬりえ




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく




働きアリ 三平方の定理




直角三角形になるとしか思えません なぜ直角二等辺三角形なのでしょうか 教えてください Clear




中2 中2 数学 二等辺三角形など 中学生 数学のノート Clear




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典




高校数学a 三角形の重心 外心 垂心の位置関係 オイラー線 の幾何的証明 受験の月
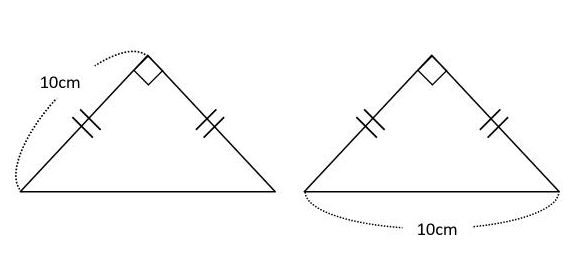



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
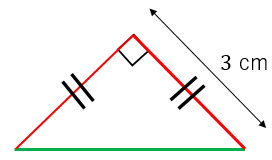



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
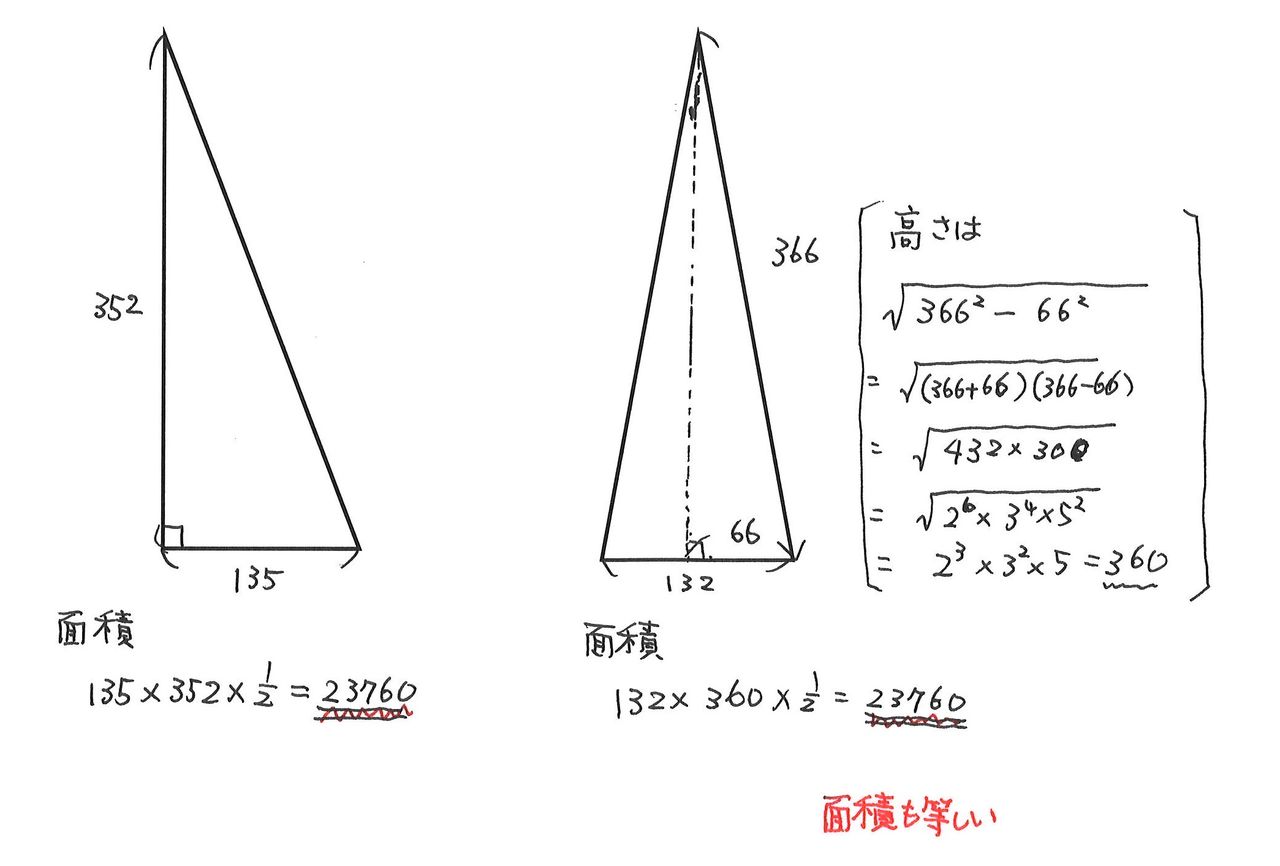



三角形のペア 大田 桐光本部校 ブログ
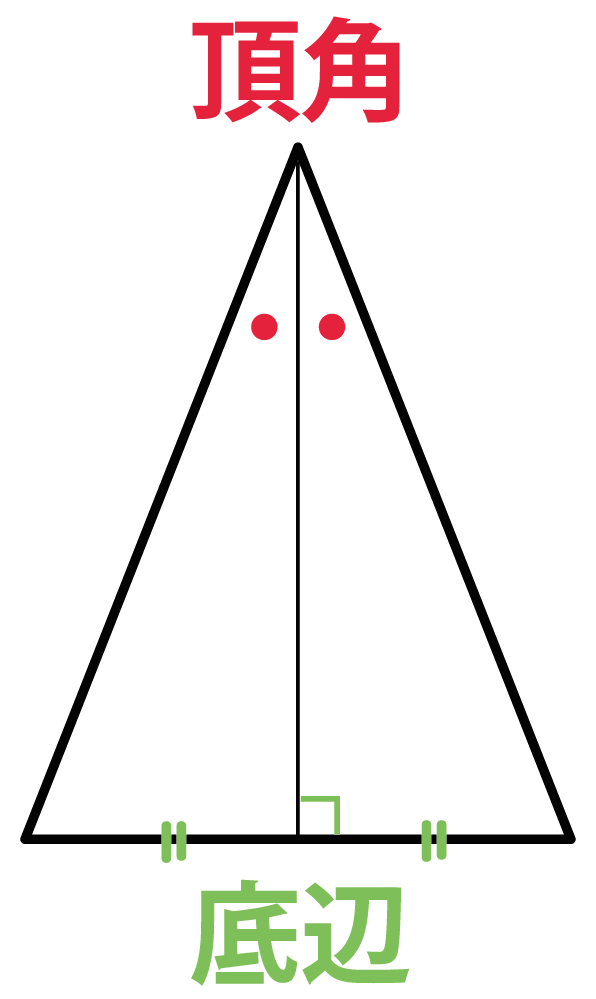



3分でわかる 二等辺三角形の2つの定理 性質 Qikeru 学びを楽しくわかりやすく




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比
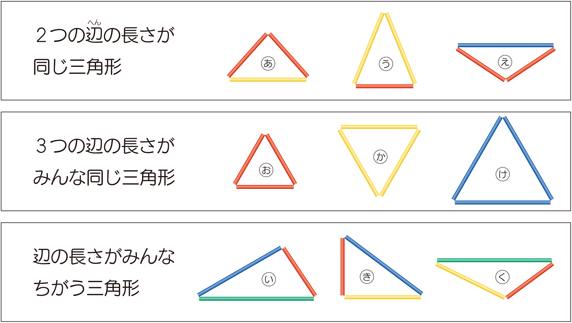



二等辺三角形と正三角形 算数用語集




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット



中学三年生 数学の問題です なぜ直角二等辺三角形を半分にす Yahoo 知恵袋




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく



直角二等辺三角形の斜辺を三等分したら直角も三等分されますよね ならない Yahoo 知恵袋




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



1




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく
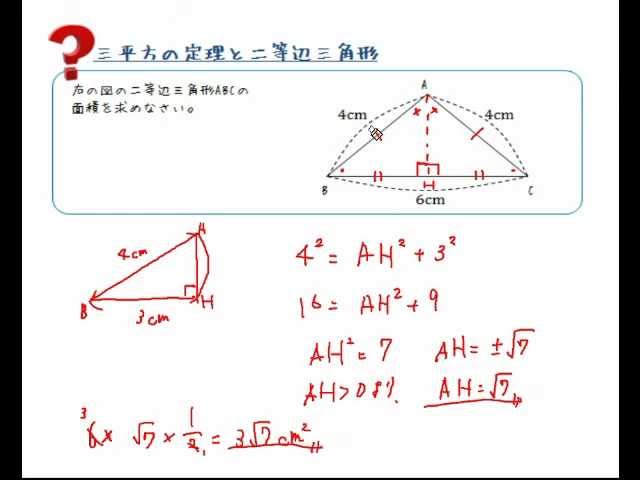



三平方の定理と二等辺三角形 Youtube
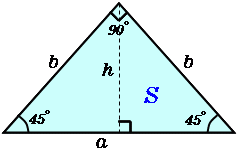



直角二等辺三角形 高精度計算サイト




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ
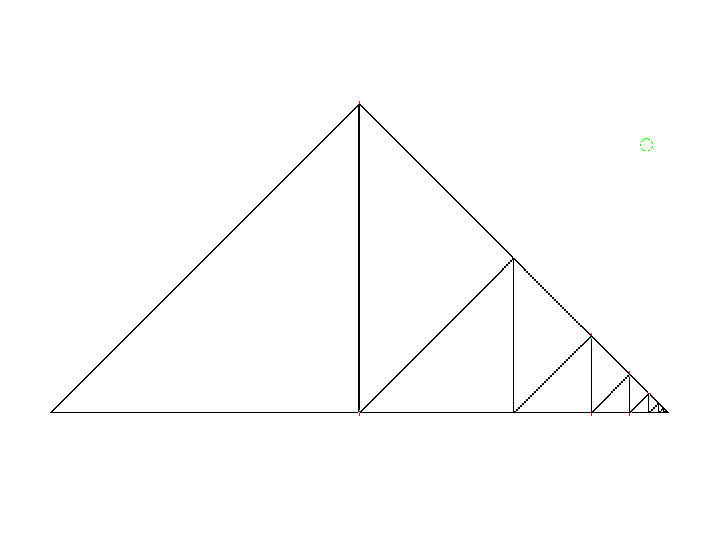



フラクタル直角二等辺三角形のギャスケットとリーマン予想の証明 発想力教育研究所 素数誕生のメカニズム
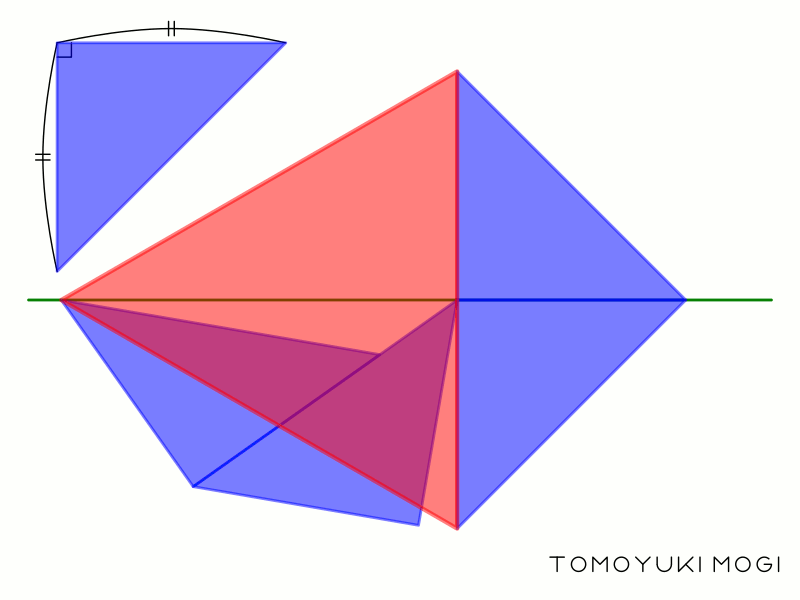



直角二等辺三角形 Wikipedia




二等辺三角形 Wikipedia




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン



3
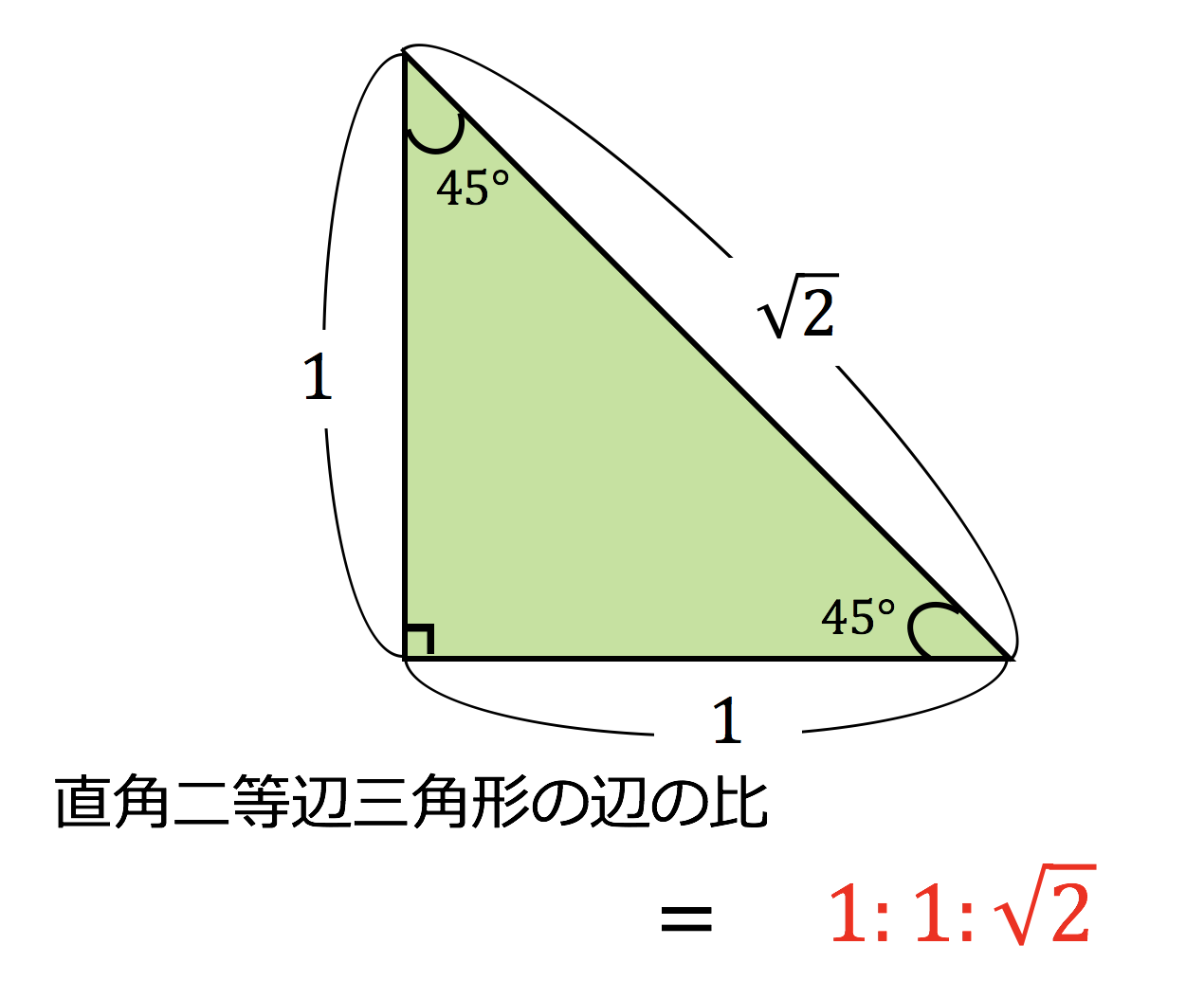



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく
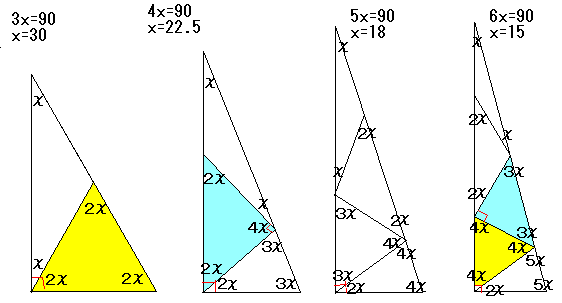



はしご直角三角形




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく
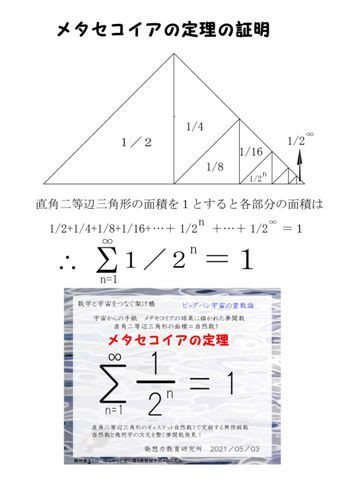



メタセコイアの定理 自然数と直角二等辺三角形の面積を繋ぐ無限級数発見 発想力教育研究所 素数誕生のメカニズム




辺の長さが全て整数となる直角三角形と二等辺三角形で周の長さも面積も共に等しい組 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明




二等辺三角形の性質 Youtube




Clear 勉強ノートまとめアプリ こんばんは 今日は友達とuberしようと思ったらドライバーさんみんな出払ってました 雪だからかな 今日紹介するのは 確認 三平方の定理 直角二等辺三角形 スクールieさんのノート 大事なところだから
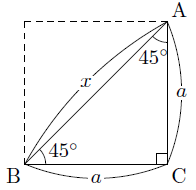



三角定規の3辺の比 まなびの学園




直角二等辺三角形の辺の求め方 直角二等辺三角形の底辺が106センチメ 数学 教えて Goo




二等辺三角形の性質の証明 頂角の二等分線 Youtube




名門国立小のカリスマ先生に聞く なんでこれがわからないの でイラっときた時の教え方 Forbes Japan フォーブス ジャパン



高校入試 英語 数学 特別な直角三角形




直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




三平方の定理の証明 外接円と直角二等辺三角形を利用した証明 Fukusukeの数学めも




ピタゴラスの第2定理発見 三平方根の定理 直角三角形の菅数論の定理 発想力教育研究所 素数誕生のメカニズム




三角比 30 45 60 もう一度やり直しの算数 数学




1 の問題で 自分の証明でも合ってますか 字が汚くてすいません Clear
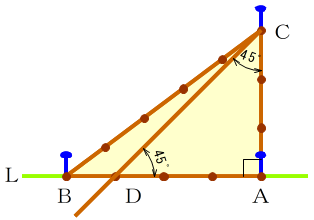



3 4 5の三角形で 本当に直角ができる Note Board



0 件のコメント:
コメントを投稿