7四角形の中の相似 相似の利用② 四角形の中の相似 815 8縮図の利用 相似の利用③ 縮図の利用 737 平行線と線分の比① 754 平行線と線分の比② 915 2中点連結定理 中点連結定理 714 中点連結定理の利用① 証明 726 中点連結定理の利用② 線分の長さ 804A B C ABC ABC の面積を表します。 三平方の定理の三次元空間バージョンです! なお,四平方の定理というと整数論におけるラグランジュの四平方和定理( →整数論の美しい定理7つ の5つ目)のことを指す場合もあるので注意して下さい。 目次 四平方の三平方の定理で高さを出せば体積を出すことができる。 例母線の長さ17cm, 底面の半径8cmの円錐の体積を求める。 17cm 8cm

三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学
三 平方 の 定理 の 利用
三 平方 の 定理 の 利用-左の直角三角形が正三角形を半分にしたものです。 3 3 辺の比は暗記で、 21√3 2 1 3 です。 次に、右の直角三角形に三平方の定理を使うと、 最後の 1 1 辺の長さが求まります。 最後の 1 1 辺の長さを y y とすると y2 =102 y 2 8 2 = 10 2 y2 64 = 100 y 2 64 三 平方 の 定理 応用 問題 平方根の数学37章三平方の定理「三平方の定理の利用」<応用問題> 組 番 名前 1右の図のように,関数 のグラフ 上に点p,χ軸上に点q(10,0)があります。 poqがop=oqの二等辺三角形に なるとき,点pの座標を求めなさい。



三平方の定理 おやじさん ネット
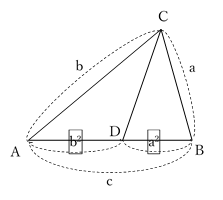
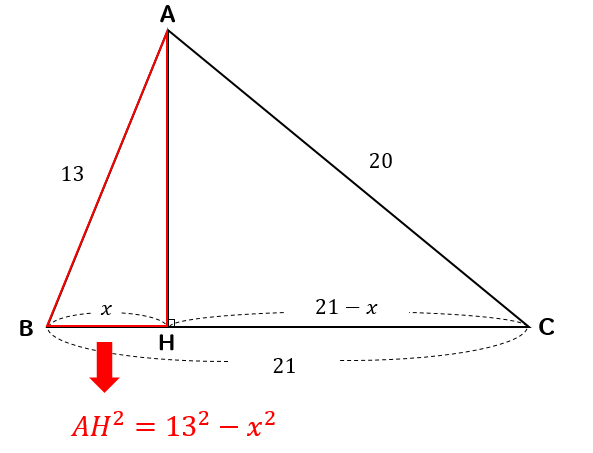
(これを三平方の定理の逆といいます.) 一番長い辺が斜辺です. ※ 直角三角形であるかどうかを調べるには, a 2 b 2 と c 2 を比較してみれば分かります. 例 三辺の長さが 3,4,5 の三角形が直角三角形であるかどうか調べるには, 5 が一番長い辺だから,プトレマイオスの定理 ・・・ トレミーの定理ともいわれる。 ※ トレミー(Ptolemaios)は、エジプト生まれのギリシャ人で、数学者、天文学者、物理学者、地理学者、和声 研究家として知られている。三平方の定理の逆ってなに?どうやって証明するの? 円錐の高さが??体積を求める問題を解説! 高さがわからない二等辺三角形の面積の求め方! 方程式を利用する発展問題を解説!←今回の記事 鈍角?鋭角三角形?三平方の定理を使って見分ける方法
の定理」を利用して 求められることに関 、定理を活 用しようとしている。 ・直角三角形の三辺の長 さの間に成り立つ関係 や、「三平方の定理」 を用いて直角三角形の うちの一辺の長さを求 め、平面図形や空間図 形の性質を考えるな ど、数学的な見方や考三平方の定理 直角三角形の3辺の 長さの間に成り立つ 関係に着目し,三平 方の定理を見いだす ことができる。 三平方の定理 の利用 図形の中に直角三 角形を見いだし, 三平方の定理を用 いることで図形の 性質などを考える ことができる。 三平方の定理には数百もの証明方法があります。今回は相似を利用した3つ目の証明方法について紹介します。 Ⅰ 三平方の定理とは 三平方の定理とは、次のような定理です。 三平方の定理(ピタゴラスの定理
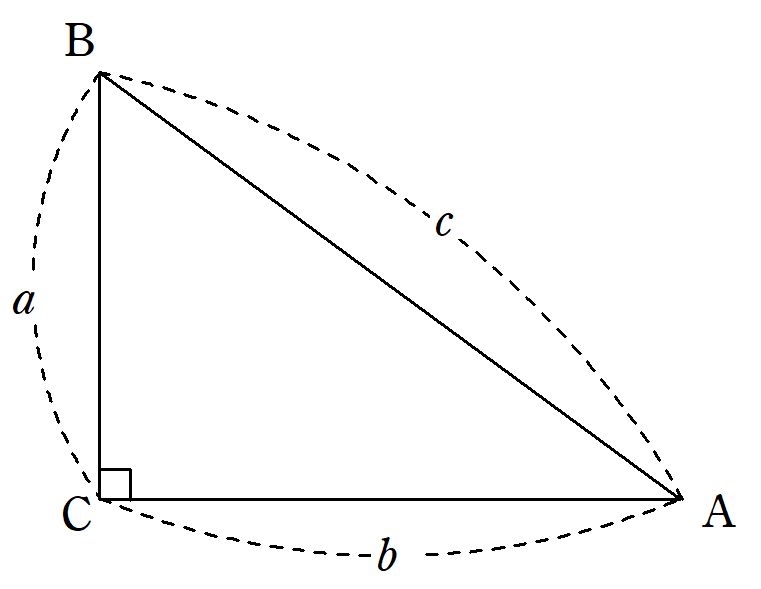
よって、これらを四平方の定理に代入すると以下のように断面積が求まる。 見事に一般的な解法と一致しました。 しかし、この四平方の定理を利用した解法は、どうみても最初に紹介した一般的な 解法より面倒な手続きとなっています。世界に1冊しかない証明集を作る徹底した探究が生む好意的学習観の醸成 ・・・・・・ 坂本 正彦 「三平方の定理の利用」の授業 母線の長さが同じでも ・・・・・・ 伊藤 勇治三平方の定理が使えるのは直角三角形である。 定理を利用する場合は図から直角三角形を探すか、補助線を書いて直角三角形を作る。 座標上での2点間の距離 いままで、座標上で斜めの長さは出せなかったが、三平方の定理を使えば出せるようになる。 a b



三平方の定理 方程式を利用する発展問題を解説 数スタ



Studydoctor三平方の定理の計算 中学3年数学 Studydoctor
三平方の定理とは、別名「ピタゴラスの定理」とも呼ばれる、とても古くからある数学の定理です。 具体的にはCを直角とする直角三角形ABCの辺 a,b,c a, b, c について、 a2 b2 = c2 a 2 b 2 = c 2ピタゴラスの定理説明器 ・・・・・・ 土井 一弘;余弦定理を交流回路で使うためには、まずベクトル図を正しく書くことを念頭においてほしい。 解きかたの順序 ① 第6図 のようにベクトル図を描く 第6図 ②余弦定理をどこに当てはめるかを考える ( oab に適用する) 2辺と挟まれる角をどこにおい




ウケる数学 三平方の定理で解く 地平線までの距離 中日新聞web



高校入試 英語 数学 三平方の定理の利用
三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題とこの定理の逆も成り立つ。すなわち、三角形の1辺の平方が他の2辺の平方の和に等しければ、始めの辺に対する頂角は直角である。この逆定理の成立によって、たとえば、辺の長さが3、4、5である三角形は3 2 +4 2 =5 2 であるから、直角三角形となる。この3 三平方の定理の逆の証明について 中学数学 3年3-1②・空間図形のなかに,三 平方の定理を利用する ための直角三角形を見 いだすことができる. ・三平方の定理やこれま でに学んだ図形の性質 を利用して,問題を解 決することができる.




三平方の定理 立体 苦手な数学を簡単に




三平方の定理 無料で使える中学学習プリント
ピタゴラスの定理の覚え方としては、 斜辺の平方は他の2辺の平方の和 が最も優れているだろう。 昨今の生徒の意識として、結果さえ覚えればOKで、その成り立ち等に関心を払わない 場合が多い。 美しい 三 平方 の 定理 円 Mathematics 三平方の定理 4 円と三平方の定理 働きアリ The 2nd 円を利用した三平方の定理の証明 数学の面白いこと 役に立つことを 三 平方 の 定理 の 利用 中3数学 三平方の定理 空間図形への利用 練習問題 三平方の定理 の問題のわからないを5分で解決 映像授業のtry It トライイット



1




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト
三平方の定理 (さんへいほうのていり)、 勾股弦の定理 (こうこげんのていり)とも呼ばれる。 ピタゴラスの定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残りの1辺の長さを知ることができる。三平方の定理の証明と使い方 三平方の定理 とは、 直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを c としたときに、 公式 a2 b2 = c2 が成り立つ という定理です。 三平方の定理には数百もの証明方法があります。今回は相似を利用した2つ目の証明方法について紹介します。 Ⅰ 三平方の定理とは 三平方の定理とは、次のような定理です。 三平方の定理(ピタゴラスの定理




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学




中3数学 三平方の定理とは 例題編 映像授業のtry It トライイット
三平方の定理(基本問題1) 例題 次の直角三角形で、xの値を求める。 x 2 6 xが斜辺なので 2 2 6 2 = x 2 x 2 = 40 x = ±2 √ 10 x > 0より x =2 √ 10 x 4 5 斜辺が5なので x 2 4 2 =5 2 x 2 = 2516 x 2 =9 x=±3 x>0より x=3 次の直角三角形で、xの値をそれぞれ求めよ。三 平方 の 定理 証明 等 積 変形 三 平方 の 定理 証明 等 積 変形 三平方の定理の証明②(ユークリッドの証明) Fukusukeの 三平方の定理が一瞬で理解できる!公式・証明から計算問題 12 双曲「幾何」の定理 mixed moss;三平方の定理の練習問題10問・解き方の解説 管理人 5月 27, 三平方の定理に関する問題は様々なパターンのものが出題されます。 初見では難しい問題が多いのですが、大体はパターンが決まっているので、ひとつずつポイントを抑えて問題に慣れて




数学 中3 63 三平方 平面図形への利用 基本編 Youtube




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース
この図からどのようにして三平方の定理が 導き出されるのだろうか。 ウモクホ数学に匹敵する学問体系を築き上げた 古代中国の学者に思いをはせながら、 証明方沵を考えてみてください。 14....補足2 三平方の定理の三次元拡張
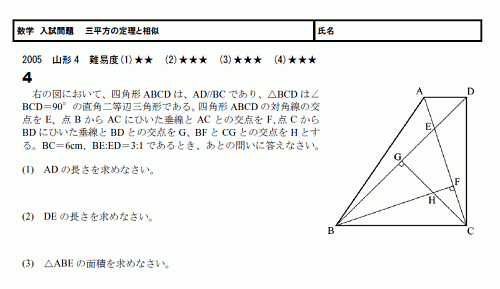



相似比の利用 三平方の定理 スタディーx



Studydoctor特別な三角形と三平方の定理 中学3年数学 Studydoctor




三平方の定理の練習問題10問 解き方の解説 数学fun




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




三平方の定理 おやじさん ネット



Studydoctor三平方の定理と四角形への利用 中学3年数学 Studydoctor



1




知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より



Studydoctor三平方の定理の利用 中学3年数学 Studydoctor
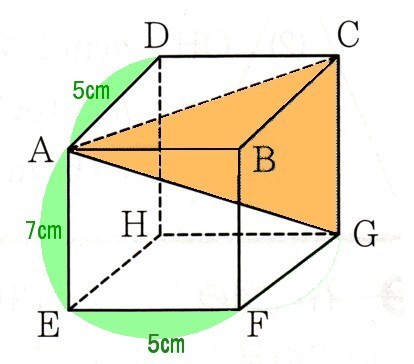



中学3年数学 三平方の定理の利用 練習問題7 1 解答 あんのん塾




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学



三平方の定理の証明 内接円の利用 Fukusukeの数学めも




7章2節1 三平方の定理の利用 数学のすすめ



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三平方の定理 空間図形への利用 Ver 2 Geogebra




三平方の定理の利用 立体 チーム エン




三平方の定理の利用 四角錐 円錐 チーム エン




三平方の定理の証明 方べきの定理の利用1 Fukusukeの数学めも




無料 中3数学 発展 応用問題 問題プリント 334 三平方の定理2
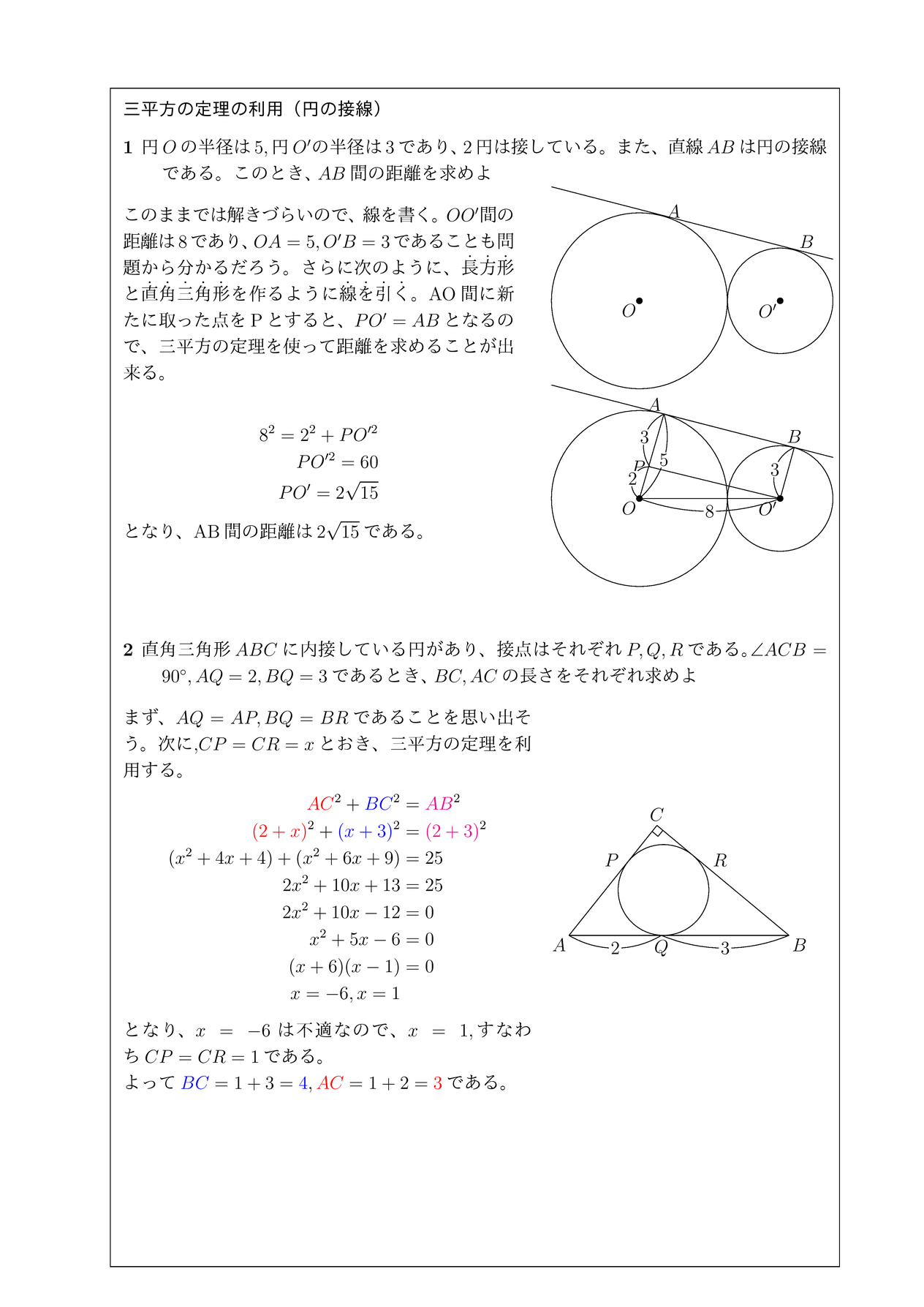



三平方の定理の利用 円の接線 チーム エン




数学 中3 65 三平方 平面図形への利用 円とのコラボ編 Youtube




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理の逆ってなに どうやって証明するの 数スタ



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 2 4
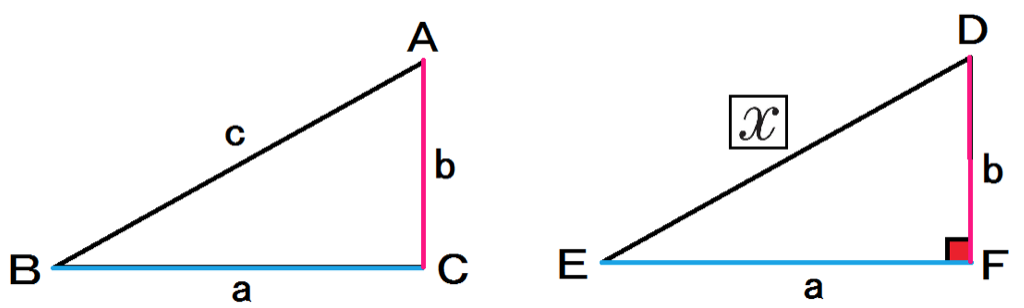



中3数学 2分でわかる 三平方の定理の逆 Qikeru 学びを楽しくわかりやすく




三平方の定理の証明と使い方




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




國三 Junior High数学的 数学 三平方の定理 筆記 Clear




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook
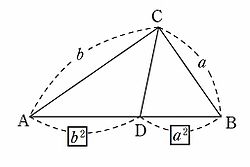



ピタゴラスの定理 Wikipedia
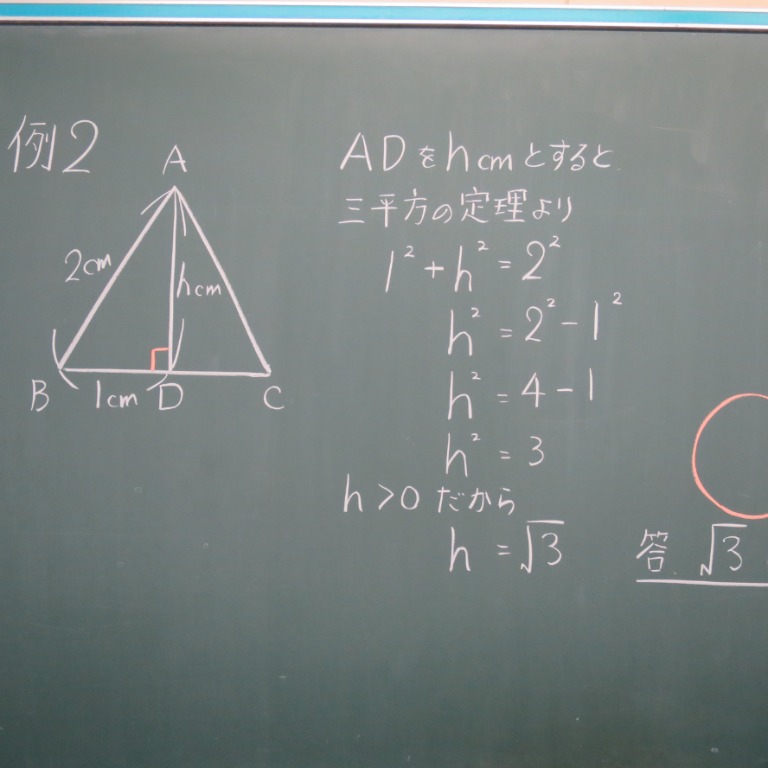



Tossランド 平面図形への利用 三角形の高さ




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも



3




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース




中3数 三平方の定理の利用 内 容 2つの三角定規の3辺の比 平面図形への利用 座標平面上の2点間の距離を求める Ppt Download




逆三平方の定理 平面版 東大カリスマ塾長 浜田一志公式ブログ 9割が伸びる 文武両道 勉強法




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく
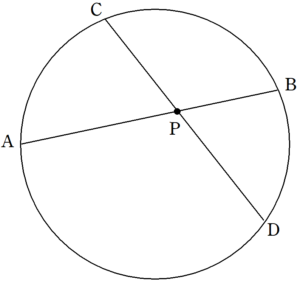



三平方の定理の証明 方べきの定理の利用1 Fukusukeの数学めも
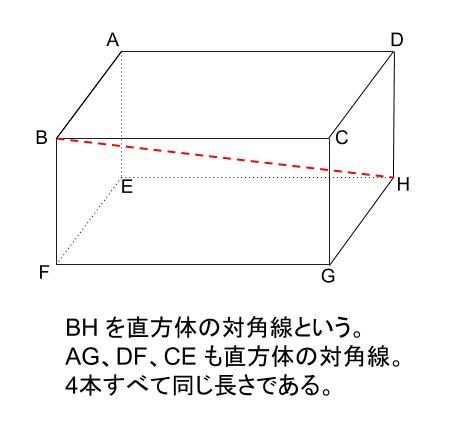



中学数学 直方体の対角線 中学数学の無料オンライン学習サイトchu Su
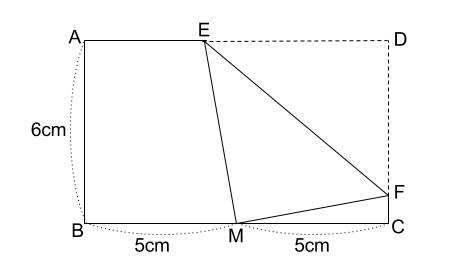



折り返しと三平方の定理 中学数学の無料オンライン学習サイトchu Su



三平方の定理
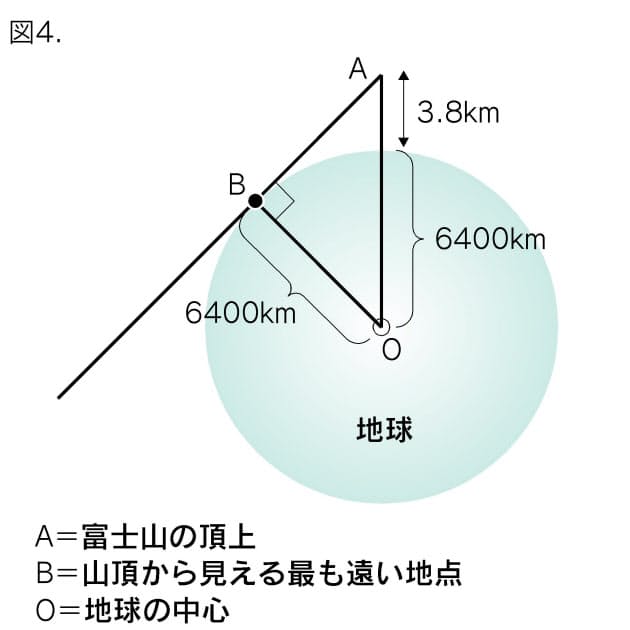



富士山やスカイツリーからどこまで見渡せるか 川の対岸までの距離 渡らずに知る方法 Nikkei Style




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理 の問題のわからないを5分で解決 映像授業のtry It トライイット




三平方の定理の逆ってなに どうやって証明するの 数スタ



Math 高校入試の難問 三平方の定理 30 60 90 1 2 3と1 2 3 30 60 90 働きアリ



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook
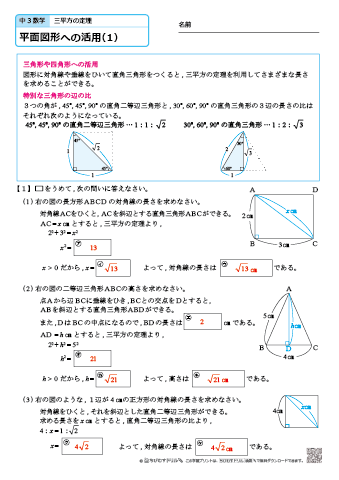



中学3年生 数学 三平方の定理 平面図形への活用 練習問題プリント ちびむすドリル 中学生




高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理の証明と使い方
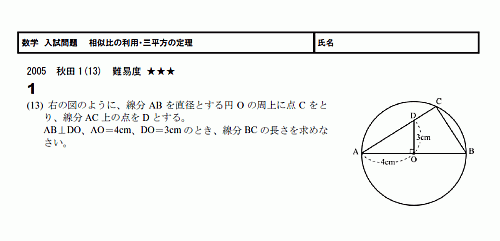



相似比の利用 三平方の定理 スタディーx




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




無料 中3数学 基本解説 解答プリント 334 三平方の定理2 比の利用




三平方の定理 覚えておきたい基本公式を解説 数スタ




三平方の定理で辺を求める Youtube



三平方の定理



名古屋市科学館 科学館を利用する 展示ガイド キーワード検索 ひ ではじまるキーワード キーワード ピタゴラスの定理 公式と図形
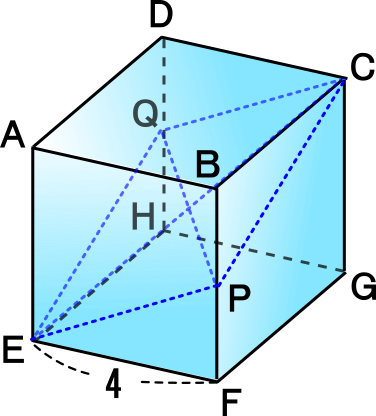



中学3年数学練習問題 三平方の定理 空間図形への利用 2
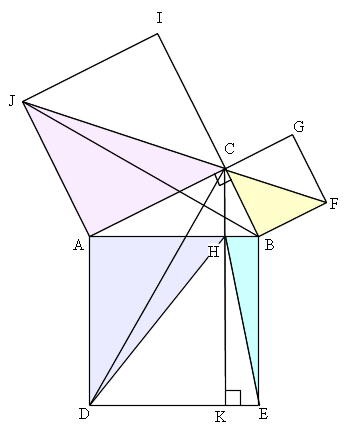



Mathematics 三平方の定理 1 三平方の定理の証明 働きアリ




中3数学 三平方の定理の逆 練習編 映像授業のtry It トライイット
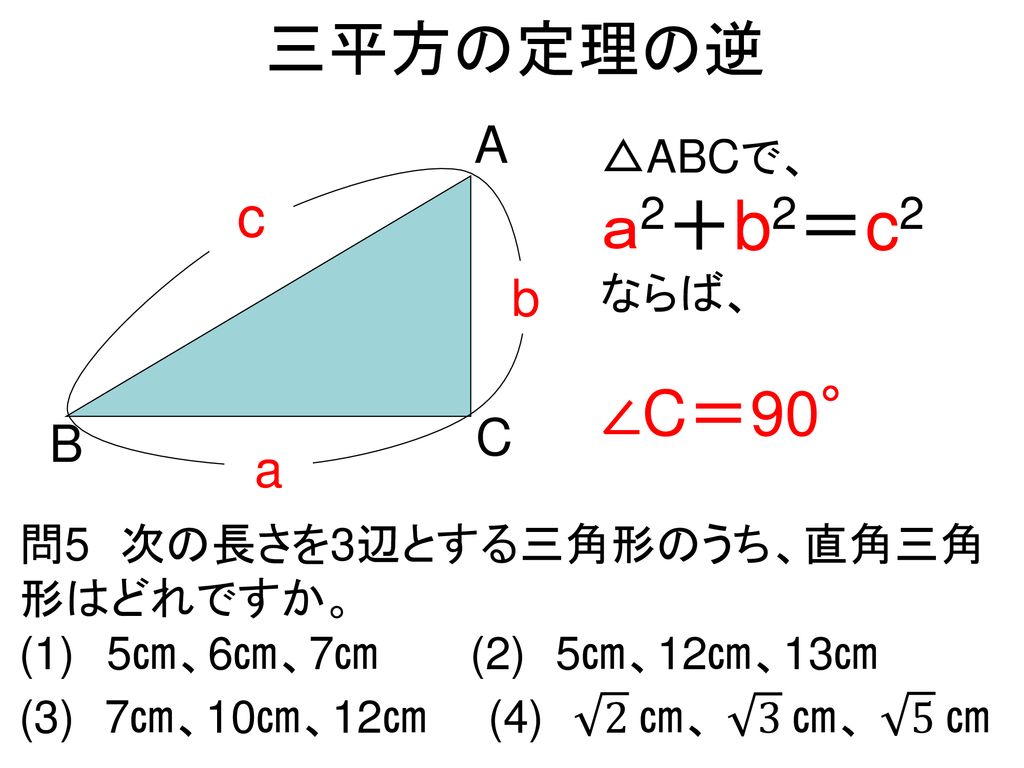



中3数 三平方の定理の計算 三平方の定理の逆 中学校 3年数学 三平方の定理 授業第2時に実施する Ppt Download




中3数学 三平方の定理 空間図形への利用 練習問題



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




数学 中3 61 三平方の定理 基本編 Youtube
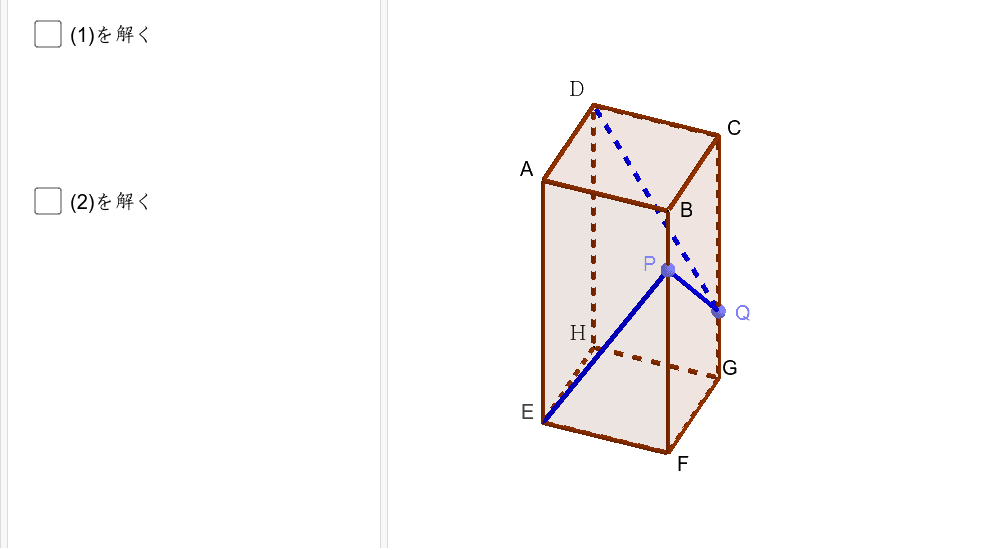



発展問題 三平方の定理の利用 Geogebra




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座




三平方の定理を利用して四角すい 円すいの体積を求める 無料で使える中学学習プリント
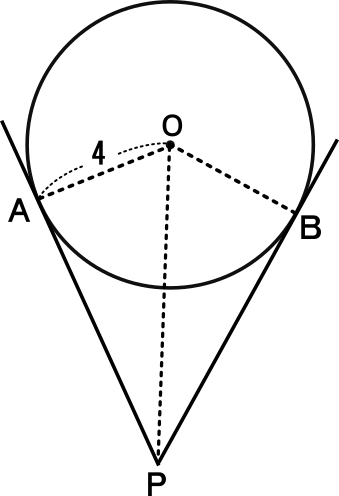



中学3年数学練習問題 三平方の定理の復習テスト



Studydoctor三平方の定理と色々な三角形の面積 中学3年数学 Studydoctor




三平方の定理 難問 中3数学 実力テスト用 高校入試過去問改 赤城 ᐡᐤᐡ




三平方の定理の利用の問題です 解説と答えを教えてくれるとありがたいです Clear




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




ピタゴラスの定理 Wikipedia




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理 相似を利用した問題 問11の 2 を教えてください Clear
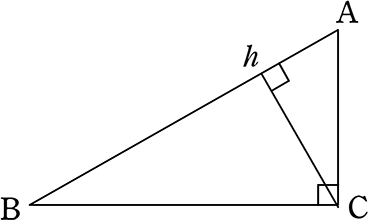



中学数学 三平方の定理
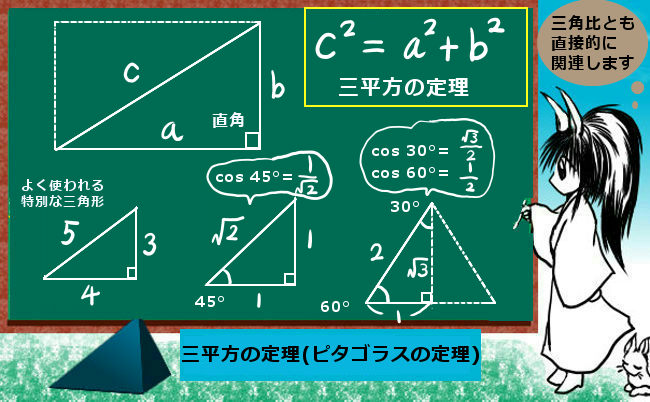



三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学



0 件のコメント:
コメントを投稿