この式から (高さ)がわかれば、 (底面積)× (高さ)= (体積)で計算できますね。 この記事の目的:錐形を求める際に「3分の1」する理由を中学生にも分かるように説明する. はじめに 錐形は3分の1 指針 ①特別な四角錐を考える ②特別な三角錐を考える ③錐体の体積の求め方の根本を考える ④体積が変わると? 最後にTwitter @tamaki_py https//twittercom/tamaki_pyサムネイル素材:"Pentagonal pyramidpng" (CC BYSA 30) https//commonswikimediaorg/wiki/FilePentagonal

19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
円錐の体積の公式
円錐の体積の公式- 斜回転体の体積を求めるための公式です。 目次 傘型分割の具体例 傘型分割の諸注意 傘型分割の簡単な説明 傘型分割の応用 傘型分割の具体例 とりあえず傘型分割を使う具体例です。 例題 y = x y=x y = x と y = x 2 − 4 x 4 y=x^24x4 y = x 2 − 4 x 4 で囲まれた図形を y = x y=x y = x の回りに回転さ円錐の体積の公式を導こう。 x2 円錐の体積 半径r の円を底面とする高さh の円錐K を考える。底面積はS = ˇr2 である。 円錐K を高さの方向にn 等分する。j = 1;2;




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su
まとめ:円錐の体積の求め方の公式はシンプル 円錐の体積の求め方はどうだったかな?? 底面積×高さ×1/3 という公式は意外とシンプルだったよね笑 最後に1/3をかけることさえ忘れなければ、ぜったいにテストでも間違えないはず。 円柱の体積の求め方を確認したところで、円柱の体積の公式についてふれておきましょう。 ある円柱において、底面の円の半径を r 、高さを h 、その円柱の体積を V とすると、V=πr 2 h 円錐の公式は超大事だから 絶対に覚えておいてくださいね!! 球の体積・表面積公式の覚え方は語呂合わせで!問題を使って解説! 平面・空間図形 129 中学数学ねじれの位置の意味とは?角柱、角錐のどこ?問題を使って解説す 平面・空間図形 129 中1作図直
円錐の側面積の公式 まずは、公式だけ図でさっと確認するよ つぎに、円錐の特徴を確認して、そのあとに側面積を求めていくよ 円錐の特徴 円錐の特徴は主に次の二つだよ 円錐は小さな円と大きな扇で成り立つ; 例えば、円錐を例に考えてみましょう。 円錐を軸に対して垂直にスライスしてできる円を積み重ねていけば、体積が求められます。 次に、平面を回転させてできる立体の体積の公式を確認しましょう。 回転させる平面が \(x\) 軸に接している場合と、\(2\) つの曲線ではさまれている場合の 三角錐,四角錐,円錐などの錐体の体積は 1 3 底面積が S S S ,高さが h h h である錐体の体積 V V V を求める公式: V = 1 3 S h V=\dfrac{1}{3} Sh V = 3 1 S h の導出を紹介します。 目次 特殊な四角錐の場合 一般の錐体の場合 積分を用いた証明 特殊な四角錐の場合 底面が一辺 2 h 2h 2 h の正方形で
円錐の体積の公式は「πr 2 h/3」です。 円柱の体積の1/3の値が円錐の体積といえます。 また円錐だけでなく「錐体」の体積は、柱体の体積の1/3となるので覚えておきましょう。 錐体(円錐、角錐)の体積は、底面積が S S 、高さが h h の錐体の体積 V V は以下の式で表します。 V = 1 3Sh V = 1 3 S h この公式を学習したときに 1 3 1 3 になる理由は知らなかったと思います。 これは特殊な四角錐の場合には比を用いて簡単に証明することが角錐・円錐の体積と表面積の公式 管理人 2月 5, 19 / 2月 15, 19 主に柱体(角柱・円柱)、錐体(角錐・円錐)、球の3種類の立体です。
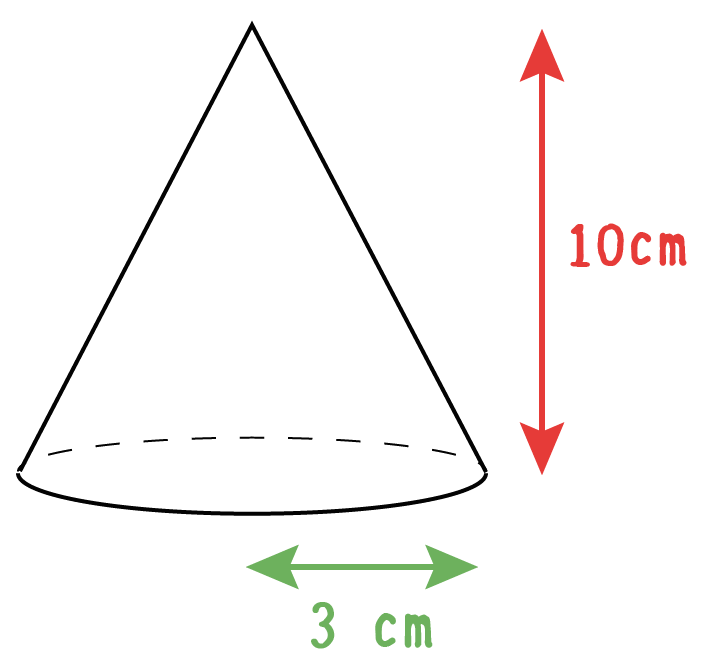



計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



球の半分と円錐を組み合わせた立体です 体積と表面積を求めよ 教え Yahoo 知恵袋
円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体円錐台の体積の計算法は知っていた(上部の円錐を引く)が、上部の円錐を考えるのが面倒だったので素早く答えがでて助かりました。 1133 男/30 底面の形が円の円錐でも、底面を小さな三角形の総和であると考えれば、 三角錐の公式が使えるので、 円錐の体積=底面積×高さ/3 になることがわかります。 (別の例) 上図のように、立方体を考えます。 立方体の中心の点を頂点とし、立方体の1つ 読者になる schoolmath's diary 16




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室
円錐の体積の公式を用いた場合 円錐の体積の公式より, V = 1 3 π r 2 h = 1 3 π × 1 2 × 1 = π 3 定積分の公式を用いた場合 定積分の基本式より, ∫ a b f (x) d x = F (x) a b = F (b) − F (a) ( F (x) は f (x) の原始関数の1である ) 求める円錐の底面積 S (x) を S (x) = π {f体積の公式、円錐の体積の公式など下記が参考になります。 体積の公式は?1分でわかる求め方と覚え方、一覧、三角柱、円柱、三角錐の体積 円錐の体積と公式は?1分でわかる公式、問題と高さの求め方、証明 100円から読める!ネット不要!円錐の体積を求める公式は、次の通りです。 V = 1 3Sh = 1 3πr2h V = 1 3 S h = 1 3 π r 2 h ここで、V は円錐の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の円の



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明




直円錐の体積 高精度計算サイト
円錐は展開図にすると,円と扇形に分離されるのでこのような公式になります. 展開図がそのまま数式になっているので非常に分かりやすく理解しやすいと思います. 体積を求める公式 V = 1 3 π r 2 h V = 1 3 π r 2 h さて,次は円錐の体積を求める公式です.例題2 一様な物質でできた,底面の半径 ,高さ の円錐の重心 底面から の位置で厚さ の円板を考えると,その半径は であり,その体積 は となる。これより重心の高さ は以下のように計算できる。 問 一様な物質でできた,半径 の半球の重心の位置を求めよ。 (こたえ) ※これは半円板の円錐 体積 公式。 公式を図解!すい体の体積、円すいの表面積の求め方 円錐の表面積や体積の求め方!すぐ分かる方法を慶応生が解説!|高校生向け受験応援メディア「受験のミカタ」 錐体 すいたい というのは、 「空間内の一点から放射状に伸びる直線によって形作られる錐状の立体図形




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学
この公式は,円柱の体積の公式 V = πr2h V = π r 2 h に 1 3 1 3 をかけたものと考えることができるが,なぜ円柱の体積に 1 3 1 3 をかけることにより円錐の体積が得られるのかを, 定積分法 と 区分求積法 を用いて説明する. すると、ふたつの錐の底面積の比は、常に1πになることがわかります。 よって、体積の比も常に1:πになります。 そして、求めたい円錐の体積は、さっき体積を求めた四角錐と高さが同じa/2であることに注目すると、 a3×1/6×π/1=πa3×a×1/2×1/3=πa3×1/6手っ取り早く円錐の体積を求めるには、この公式に値を代入すればよいだけです。 このページの続きでは、公式の導出方法も説明していますが、公式を使わずに、順番に計算する方法もお示ししますので、みなさんの必要に応じて使い分けてください。 もくじ 円錐の表面積を求める公式 公式




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
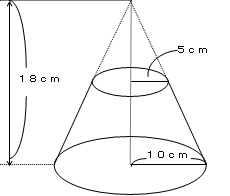
円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 Sこの立体の体積は (cm 3 ) 外側の体積 160π (cm3)から空洞になっている内側の体積 40π (cm3)を引くと V=1π (cm3) 大きな円錐の体積は π×6 2 ×10÷3=1π (cm3) 上端の円錐の底面の半径 ( x とおく)は,比例(相似)の関係を使って求めることができる.縦:横 x 5x=106;n に対して,頂点からの距離 が j n h である,底面と平行な平面で円錐K を切ったときの切口は




公式を図解 すい体の体積 円すいの表面積の求め方




円錐の体積ってなんであの公式なの Webty Staff Blog
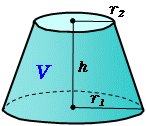
No012 円錐の体積と表面積 円錐の体積 V m 3 円錐の底面の半径 r m 円錐の高さ h m 円錐の母線の長さ l m 円錐の底面の面積 S 1 m 2 扇形の中心角 θ deg 扇形の周の長さと円錐の底面の円周の長さは等しい 扇形の面積 S 2 m 2 円錐の表面積 S m 2 2円錐台の体積の公式 S:はじめまして。いつもホームページ読ませていただいてます。 さて、円錐の体積で教えてほしいことがあります。 円錐を底面からhの高さで底面と水平にスパッと切った時の体積なのですが、真横からみると台形になる。この立体の底面(大きい円)の面積をa、上面 円錐台の体積の公式 S:はじめまして。いつもホームページ読ませていただいてます。 さて、円錐の体積で教えてほしいことがあります。 円錐を底面からhの高さで底面と水平にスパッと切った時の体積なのですが、真横からみると台形になる。体積 V = 1 3 π ( r 1 2 r 1 r 2 r 2 2) h円錐台(え




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




公式を図解 すい体の体積 円すいの表面積の求め方
円錐台の体積 110 /138件 表示件数 5 10 30 50 100 0 1 1632 男 / 歳未満 / 会社員・公務員 / 非常に役に立った / 使用目的 拡底杭の拡底部の計算 ご意見・ご感想 拡底部の円錐台状の箇所に入れるコンクリート量を計算しました。また,中心角は上の④の公式を用いると, 4 8 ×360°=180° と求められる。 答 48∏cm2 142 次の図の円錐の体積を求めよ。 ⑴ ⑵ ⑶ ¬=2∏r 115中学の数学幾何I_H_p0357indd 495中学の数学幾何I_H_p0357indd 49 626 PM6129 626 PM 2章 空間図形 50 144 次の図の円錐の表面積を求めよ。 ⑴ ⑵ ⑶ 146
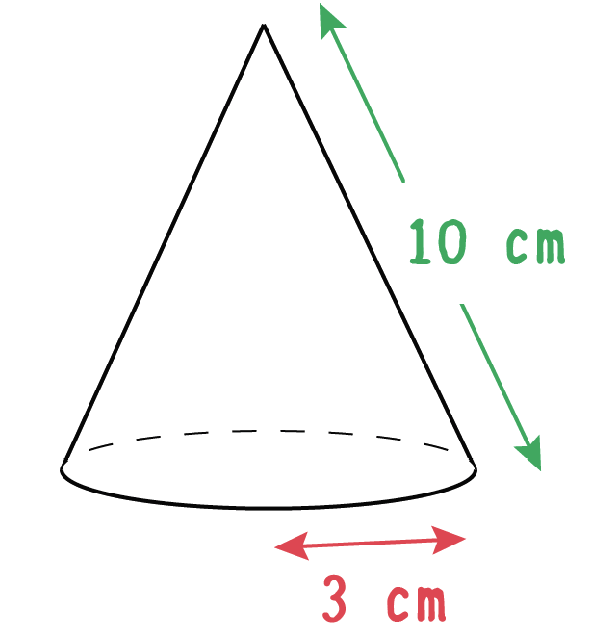



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



円錐 円すいの体積と公式 体積計算機




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の表面積 Youtube




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
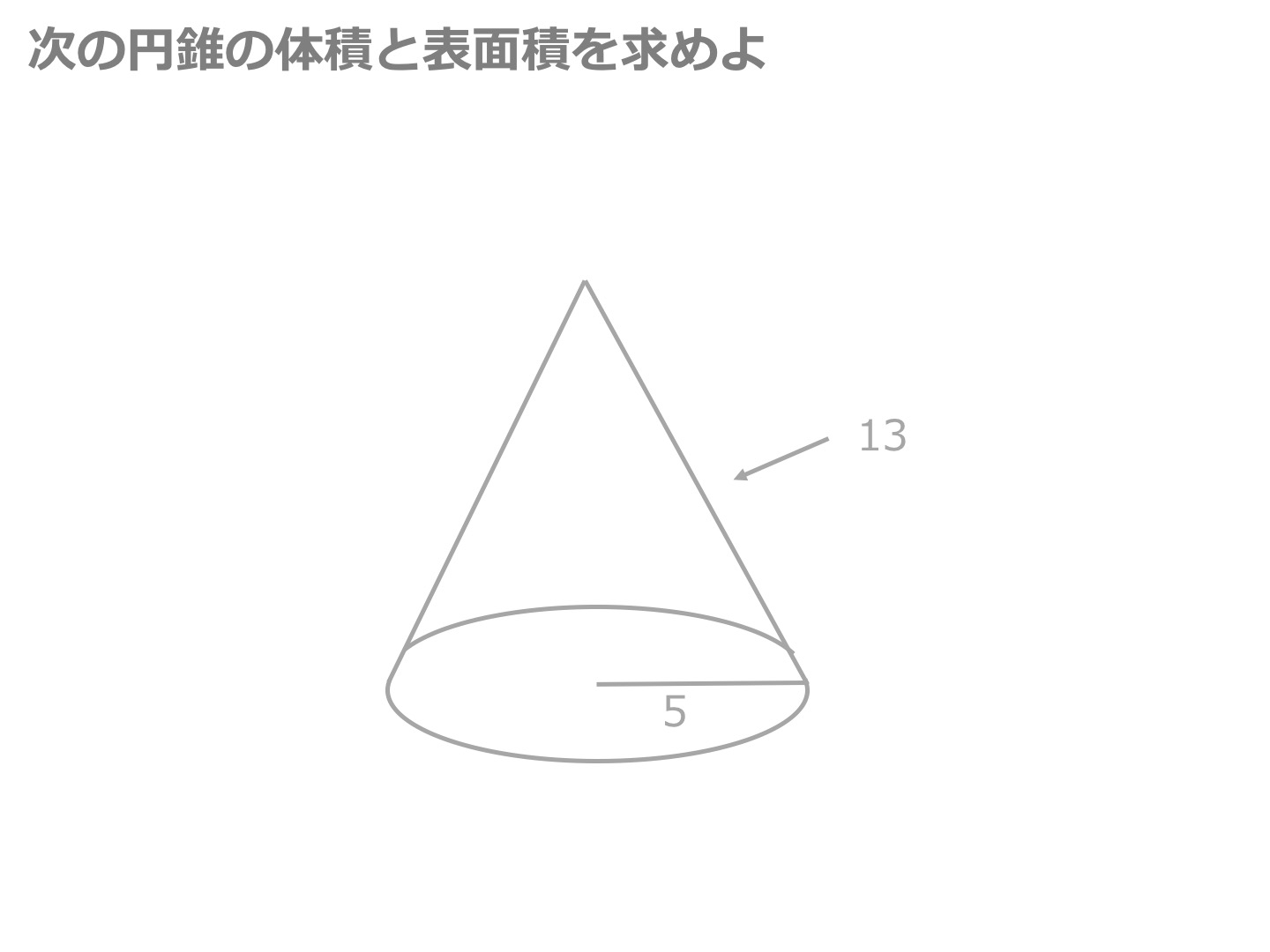



3分でわかる 円錐の体積 表面積の求め方 合格サプリ



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明




中3 三角形の相似 円錐の体積比 日本語版 Youtube




円錐の体積の求め方 公式 小学生 中学生の勉強



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明




円錐は1 3 中学生に分かるように真剣に考えてみた うちーノート




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室



1
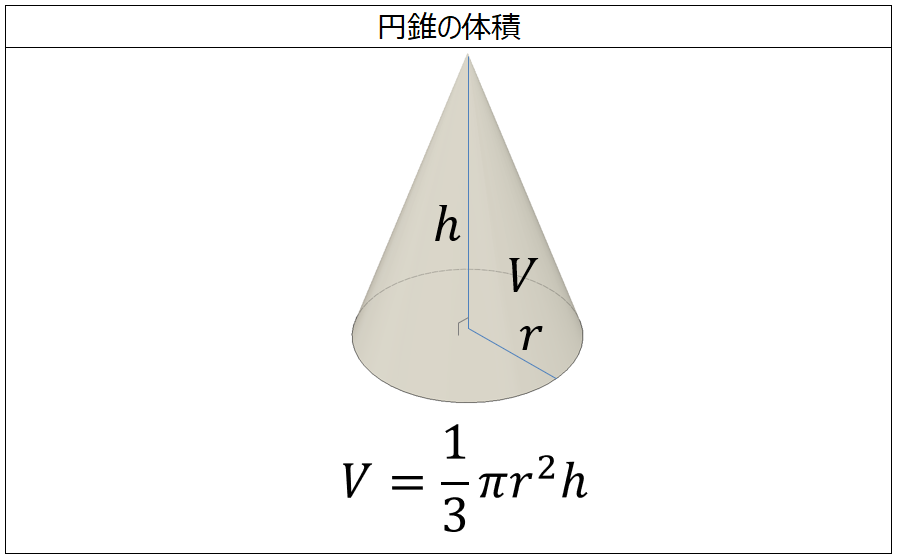



体積の計算 円錐 製品設計知識




円錐の表面積 Youtube



体積 円錐台の体積を求める 子供に教える算数のツボ




円錐の体積ってなんであの公式なの Webty Staff Blog



1



円錐とは 体積 表面積の公式や求め方 受験辞典




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者



双円錐 Wikipedia




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




球の表面積と体積の公式 数学fun




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su




どうして1 3なの 錐の体積の公式の求め方 まなべーと




円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順



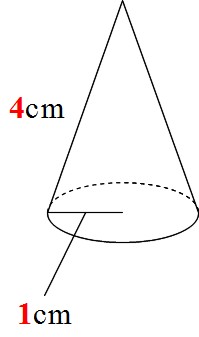
円錐の体積の求め方を教えてください 底面の直径と母線の長さがともに8c Yahoo 知恵袋




高校入試対策数学 円錐に関する対策問題 Pikuu




高さの分からない円すい展開図 どうやって立体の体積を求めるの




この問題の円錐の底面積の半径の求め方を教えてください Clear




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




毎日問題を解こう 27 苦手な数学を簡単に




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典



円錐台の体積 高精度計算サイト




3分でわかる 円錐の体積 表面積の求め方 合格サプリ




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



3




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




円錐の体積を求める Youtube



数学公式の最強裏技一覧 中学生や高校生の方はぜひ見て 三重の個人契約家庭教師




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題



地図の体積計測




空間図形14 円すい台の体積 Youtube




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト



Studydoctor円錐の表面積の求め方 中学1年数学 Studydoctor




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積の求め方 公式と計算例



1
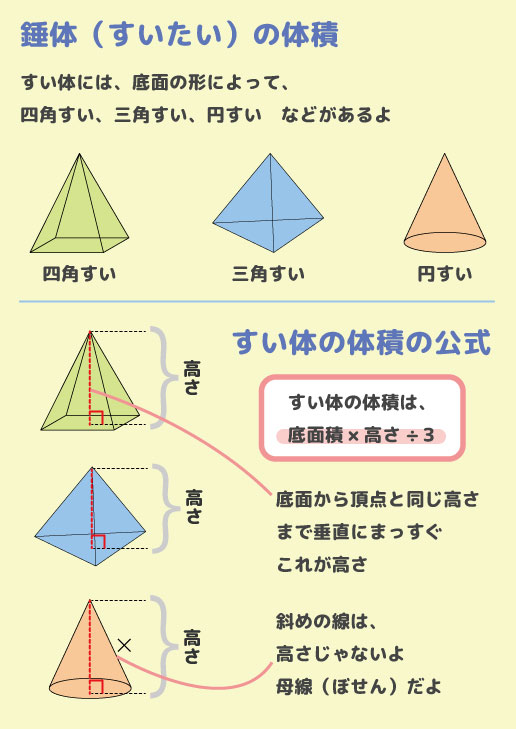



中1数学 すい体の体積と円すいの表面積 数学検定5級 お家でお勉強




相似比と体積比 円錐台 中学3年数学 Youtube




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




体積の求め方 計算公式一覧




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun




公式を図解 すい体の体積 円すいの表面積の求め方




円錐の表面積 側面積 体積の求め方教えてください Clear




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




円錐の体積ってなんであの公式なの Webty Staff Blog




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




中1 数学 中1 立体の表面積 Youtube




円錐の表面積の求め方 公式と計算例




公式を図解 すい体の体積 円すいの表面積の求め方




三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ



円錐 体積の比較 中学から数学だいすき




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




円錐の体積の求め方 公式と計算例




角錐 円錐の体積 Youtube




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円錐の体積の求め方 公式 小学生 中学生の勉強




積分を用いた円錐の体積公式の導出 頭の整理




角錐 円錐の体積と表面積の公式 数学fun




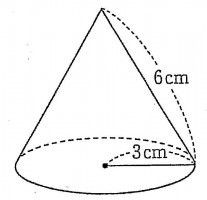
半径5分の12cm 高さ6cmの双円錐の体積を求めるのに Clear



0 件のコメント:
コメントを投稿